
 如图,在?ABCD中,E为AD中点,CE交BA延长线于F,
如图,在?ABCD中,E为AD中点,CE交BA延长线于F,科目:初中数学 来源: 题型:解答题
 2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 12 | 13 | 14 | 15 | 10 | 16 | 13 | 11 | 15 | 11 |
| 乙 | 11 | 16 | 17 | 14 | 13 | 19 | 6 | 8 | 10 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y1=2x+2及直线y2=-x+5,.
已知直线y1=2x+2及直线y2=-x+5,.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
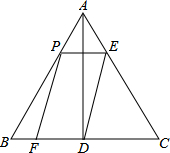 如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6).
如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com