Question

有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有2个完全相同的小球，分别标有数字﹣1，﹣2．现从甲袋中随机抽取一个小球，将标有的数字记录为x，再从乙袋中随机抽取一个小球，将标有的数字记录为y，确定点M的坐标为（x，y）．

（1）用树状图或列表法列举点M所有可能的坐标；

（2）求点M（x，y）在二次函数y=x²﹣2x﹣2的图象上的概率．

Answer 1

【考点】列表法与树状图法；二次函数图象上点的坐标特征．

【专题】计算题．

【分析】（1）画树状图可展示所有6种等可能的结果数；

（2）根据二次函数图象上点的坐标特征可判断M（x，y）在二次函数y=x²﹣2x﹣2的图象上的结果数，然后根据概率公式求解．

【解答】解：（1）画树状图为：

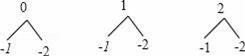
共有6种等可能的结果数，它们为（0，﹣1），（0，﹣2），（1，﹣1），（1，﹣2），（2，﹣1），（2，﹣2）；

（2）点M（x，y）在二次函数y=x²﹣2x﹣2的图象上的结果数为2，

所以点M（x，y）在二次函数y=x²﹣2x﹣2的图象上的概率==．

【点评】本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．