
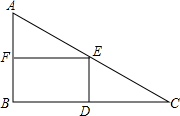
 2015年6月27日,四川共青图雨城区委在中里镇文化馆举办了第二期青年剪纸培训,参加培训的小王想把一块Rt△ABC废纸片剪去一块矩形BDEF纸片,如图所示,若∠C=30°,AB=10cm,则该矩形BDEF的面积最大为( )
2015年6月27日,四川共青图雨城区委在中里镇文化馆举办了第二期青年剪纸培训,参加培训的小王想把一块Rt△ABC废纸片剪去一块矩形BDEF纸片,如图所示,若∠C=30°,AB=10cm,则该矩形BDEF的面积最大为( )| A. | 4$\sqrt{3}$cm3 | B. | 5$\sqrt{3}$cm3 | C. | 10$\sqrt{3}$cm3 | D. | 25$\sqrt{3}$cm3 |
分析 先根据锐角三角函数的定义求出BC的长,根据EF∥BC可知△AEF∽△ACB,故∠AEF=∠C=30°,
设EF=x,则AF=$\frac{\sqrt{3}}{3}$x,故AB=10-$\frac{\sqrt{3}}{3}$x,再由矩形的面积公式即可得出结论.
解答 解:∵Rt△ABC中,∠C=30°,AB=10cm,
∴BC=$\frac{AB}{tan30°}$=$\frac{10}{\frac{\sqrt{3}}{3}}$=10$\sqrt{3}$cm.
∵EF∥BC,
∴∠AEF=∠C=30°,
设EF=x,则AF=$\frac{\sqrt{3}}{3}$x,
∴BF=10-$\frac{\sqrt{3}}{3}$x,
∴S矩形BDEF=BD•BF=x•(10-$\frac{\sqrt{3}}{3}$x)=-$\frac{\sqrt{3}}{3}$x2+10x(0<x<10$\sqrt{3}$),
∴当x=-$\frac{10}{2×\frac{\sqrt{3}}{3}}$=5$\sqrt{3}$时,S最大=$\frac{-{10}^{2}}{4×(-\frac{\sqrt{3}}{3})}$=25$\sqrt{3}$cm2.
故选D.
点评 本题考查的二次函数与三角函数的应用,根据题意列出关于x的二次函数,利用二次函数的最值问题求解是解答此题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,为测量河两岸相对两电线杆A、B间的距离,在距A点16m的C处(AC⊥AB),测得∠ACB=52°,则A、B之间的距离应为( )
如图,为测量河两岸相对两电线杆A、B间的距离,在距A点16m的C处(AC⊥AB),测得∠ACB=52°,则A、B之间的距离应为( )| A. | 16sin52°m | B. | 16cos52°m | C. | 16tan52°m | D. | $\frac{16}{tan52°}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{30}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com