
如图1,在△ABC,∠A=45°,延长CB至D,使得BD=BC.
(1)若∠ACB=90°,求证:BD=AC;
(2)如图2,分别过点D和点C作AB所在直线的垂线,垂足分别为E、F,求证:DE=CF;
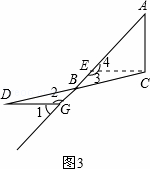
(3)如图3,若将(1)中“∠ACB=90°”去掉,并在AB延长线上取点G,使得∠1=∠A”.试探究线段AC、DG的数量与位置关系.

(1)证明:∵∠A=45°,∠ACB=90°,∴∠ABC=∠A=45°,∴AC=BC,
∵BD=BC,∴BD=AC;
(2)证明:∵DE⊥AB,CF⊥AB,∴∠E=∠CFB=90°,
∵∠DBE=∠CBF,BD=BC,∴△DBE≌△CBF(AAS),∴DE=CF;
(3)解:DG=AC,DG⊥AC.
证明:过点C作CE∥DG交AB于点E,∴∠2=∠3,
∵∠1+∠2=180°,∠3+∠4=180°,∴∠1=∠4,∵∠1=∠A,∴∠4=∠A,∴AC=CE,
∵BD=BC,∠EBC=∠GBD,∠2=∠3,
∴△DBG≌△CBE(AAS),∴CE=DG,∴DG=AC.
∵∠A=45°,∴∠4+∠A=90°,∴∠ACE=90°,∴AC⊥CE,∴AC⊥DG.
 ∴DG=AC,DG⊥AC.
∴DG=AC,DG⊥AC.


科目:初中数学 来源: 题型:
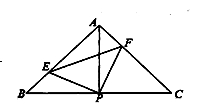
如图,已知△ABC中,AB=AC=2,∠BAC=90º,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;
②△EPF是等腰直角三角形;③S四边形AEPF=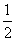 S△ABC;
S△ABC;
④EF的最小值为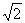 .上述结论始终正确的有( )
.上述结论始终正确的有( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1所示,△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E.△ABC的周长为12,△ADE的周长为6.则BC的长为( )
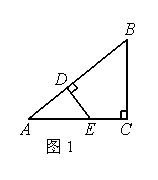 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6
查看答案和解析>>
科目:初中数学 来源: 题型:
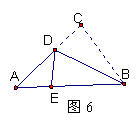
如图6,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E,折痕为BD,则 △AED的周长为 。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com