
分析 (1)根据“超过200元而不足500元的按9折优惠”可得:200×90%=180元,由于第一次购物134元<180元,故不享受任何优惠;由“超过500元,其中500元按9折优惠,超过部分8折优惠”可知500×90%=450元,490>450元,故此人购物享受“超过500元,其中500元按9折优惠,超过部分8折优惠”,设他所购价值x元的货物,首先享受500元钱时的9折优惠,再享受超过500元的8折优惠;
(2)节省的钱数=不打折花费-实际交费;
(3)(用两次购物的不打折的消费-500元)×80%+500×90%,可算出两次购物合为一次购买实际应付费用,再与他两次购物所交的费用进行比较即可.
解答 解:(1)①因为134元<200×90%=180元,所以该人不享受优惠;
②因为第二次付了490元>500×90%=450元,所以该人享受超过500元,其中500元按9折优惠,超过部分8折优惠.
设他所购价值x元的货物,
则90%×500+(x-500)×80%=490,
得x=550,
答:此人两次购物时,所购物品的标价分别为134元、550元;
(2)550-490=60(元);
答:在这次活动中他节省了60元钱;
(3)500×90%+(550+134-500)×80%=597.2(元),
134+490=624(元),
∵597.2<624,
∴此人将这两次购物合为一次购买更节省.
点评 此题主要考查了实际生活中的折扣问题,关键是运用分类讨论的思想:分析清楚付款打折的两种情况.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3\frac{1}{4}}$=2$\sqrt{13}$ | B. | $\sqrt{\frac{2m}{3n}}$=3n$\sqrt{6mn}$ | ||
| C. | $\sqrt{\frac{a}{{b}^{2}}+\frac{b}{{a}^{2}}}$=($\frac{1}{a}$+$\frac{1}{b}$)$\sqrt{a+b}$ | D. | $\sqrt{\frac{2{x}^{2}}{27(x-1)^{2}}}$=$\frac{x}{9(x-1)}$$\sqrt{6}$(x>1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
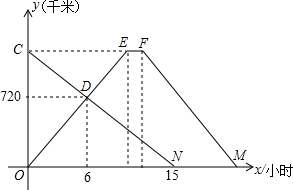 快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.如图表示的是两车离A站的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息,解答下列问题:
快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.如图表示的是两车离A站的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com