
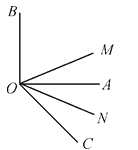
【题目】如图,∠AOB是直角,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)当∠AOC=40°,求出∠MON的大小,并写出解答过程理由;
(2)当∠AOC=50°,求出∠MON的大小,并写出解答过程理由;
(3)当锐角∠AOC=α时,求出∠MON的大小,并写出解答过程理由.
【答案】(1)45°;(2)45°;(3)45°.
【解析】试题分析:(1)根据∠AOB是直角,∠AOC=40°,可得∠AOB+∠AOC=90°+40°=130°,再利用OM是∠BOC的平分线,ON是∠AOC的平分线,即可求得答案.
(2)方法同(1);
(3)根据∠MON=∠MOC-∠NOC,又利用∠AOB是直角,可得∠MON=![]() ∠AOB=45°.
∠AOB=45°.
试题解析:(1)∵∠AOB是直角,∠AOC=40°,
∴∠AOB+∠AOC=90°+40°=130°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,
∴∠MOC=![]() ∠BOC=65°,∠NOC=
∠BOC=65°,∠NOC=![]() ∠AOC=20°.
∠AOC=20°.
∴∠MON=∠MOC-∠NOC=65°-20°=45°,
(2)∵∠AOB是直角,∠AOC=50°,
∴∠AOB+∠AOC=90°+50°=140°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,
∴∠MOC=![]() ∠BOC=70°,∠NOC=
∠BOC=70°,∠NOC=![]() ∠AOC=25°.
∠AOC=25°.
∴∠MON=∠MOC-∠NOC=70°-25°=45°;
(3)∵∠AOB=90°,∠AOC=α,
∴∠AOB+∠AOC=∠BOC=90°+α.
∵OM平分∠BOC,
∴∠MOC=![]() ∠BOC=45°+
∠BOC=45°+![]() α.
α.
∵ON是∠AOC的角平分线,
∴∠1=![]() ∠AOC=
∠AOC=![]() α.
α.
∴∠MOC-∠1=45°+![]() α-
α-![]() α=45°.
α=45°.
即∠MON=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(﹣2,3)向下平移4个单位得到点P′,则点P′所在象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,运算正确的是( )
A.x2+x2=x4B.3xmyn﹣2xmyn=1
C.﹣6x2y4÷3x2y4=﹣2D.4x2y35x3y2=9x5y5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
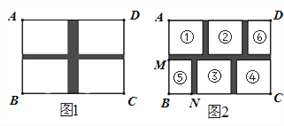
【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道(通道面积不超过总面积的![]() ),其余部分铺上草皮.
),其余部分铺上草皮.
(1)如图1,若设计两条通道,一条横向,一条纵向,4块草坪为全等的长方形,每块草坪的两边之比为3:4,并且纵向通道的宽度是横向通道宽度的2倍,问横向通道的宽是多少?
(2)如图2,为设计得更美观,其中草坪①②③④为全等的正方形,草坪⑤⑥为全等的长方形(两边长BN:BM=2:3),通道宽度都相等,问:此时通道的宽度又是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价60元,厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款.
现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若按方案①购买夹克和T恤共需 元(用含x的式子表示),若按方案②购买夹克和T恤共需 元(用含x的式子表示)
(2)若x=40,通过计算说明按方案①,②,哪种方案购买较为合算?
(3)当购买多少件T恤时,按以上两种方案购买所付价钱一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家电信公司推出两种移动电话计费方法:计费方法![]() 是每月收月租费
是每月收月租费![]() 元,通话时间不超过
元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分的按每分钟
分的按每分钟![]() 元加收通话费;计费方法
元加收通话费;计费方法![]() 是每月收月租费
是每月收月租费![]() 元,通话时间不超过
元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分的按每分钟
分的按每分钟![]() 元加收通话费.设通话时间为
元加收通话费.设通话时间为![]() 分.
分.
(![]() )用代数式表示通话
)用代数式表示通话![]() 分钟的通话费用.
分钟的通话费用.
(![]() )用计费方法
)用计费方法![]() 的用户一个月累计通话
的用户一个月累计通话![]() 分钟所需的话费,若改用计费方法
分钟所需的话费,若改用计费方法![]() ,则可多通话多少分钟?
,则可多通话多少分钟?
(![]() )按
)按![]() ,
, ![]() 两种计费方法,所需的话费会相等吗?如果会,请指出相等的时间.
两种计费方法,所需的话费会相等吗?如果会,请指出相等的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com