Question

【题目】已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．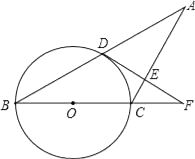

求证：
（1）AD=BD；
（2）DF是⊙O的切线．

Answer 1

【答案】
（1）证明：证法一：连结CD，

∵BC为⊙O的直径
∴CD⊥AB
∵AC＝BC
∴AD＝BD
证法二：连结CD，
∵BC为⊙O的直径
∴∠ADC＝∠BDC＝90°
∵AC＝BC，CD＝CD
∴△ACD≌△BCD
∴AD＝BD
（2）证明：证法一：连结OD，

∵AD＝BD，OB＝OC
∴OD∥AC
∵DE⊥AC
∴DF⊥OD
∴DF是⊙O的切线．
证法二：连结OD，
∵OB=OD
∴∠BDO＝∠B
∵∠B＝∠A
∴∠BDO=∠A
∵∠A+∠ADE＝90°
∴∠BDO＋∠ADE＝90°
∴∠ODF=90°
∴DF是⊙O的切线．
【解析】（1）连接DC，可构造直径所对的90度的圆周角，再利用等腰三角形的性质，可证出结论；（2）连接OD，证ODDF，利用直径的性质和等腰三角形的性质可证出结论.