
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,AE=CF,连接DE、BE、BF、DF.
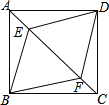
(1)求证:四边形BEDF为菱形;
(2)若菱形BEDF的边长为2![]() ,AE=2,求正方形ABCD的边长.
,AE=2,求正方形ABCD的边长.
【答案】(1)见解析;(2)AB=4![]() .
.
【解析】
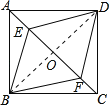
(1)连结BD交AC于点O,证明OE=OF,得到四边形BEDF为平行四边形,再证明EB=ED,得到四边形BEDF是菱形;
(2)根据△EOB是直角三角形,构造方程求出OA,根据正方形性质求出AB即可.
(1)证明:连结BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形;
(2)设AO=x,则OE=x﹣2,
在Rt△EOB中,BE2=BO2+OE2,
即20=x2+(x﹣2)2,
解得:x=4或﹣2(舍),
∴AO=4,
∴![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
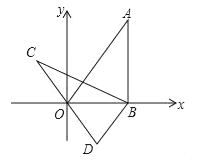
【题目】如图,在平面直角坐标系xOy中,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为_____.
经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
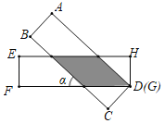
【题目】如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合.当两张纸片交叉所成的角α最小时,sinα等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是经过点A的一条直线,点C是直线
是经过点A的一条直线,点C是直线![]() 左侧的一个动点,且满足
左侧的一个动点,且满足![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点C顺时针旋转60°,得到线段
绕点C顺时针旋转60°,得到线段![]() ,在直线
,在直线![]() 上取一点B,使
上取一点B,使![]() .
.
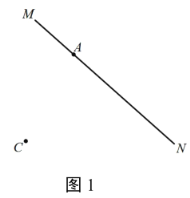
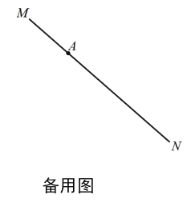
(1)若点C位置如图1所示.
①依据题意补全图1;
②求证:![]() ;
;
(2)连接![]() ,写出一个
,写出一个![]() 的值,使得对于任意一点C,总有
的值,使得对于任意一点C,总有![]() ,并证明.
,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点A(﹣5,0)作垂直于x轴的直线AB,直线y=x+b与双曲线y=﹣![]() 相交于点P(x1,y1)、Q(x2,y2),与直线AB相交于点R(x3,y3).若y1>y2>y3时,则b的取值范围是( )
相交于点P(x1,y1)、Q(x2,y2),与直线AB相交于点R(x3,y3).若y1>y2>y3时,则b的取值范围是( )
A.b>4B.b>4或b<﹣4
C.﹣![]() <b<﹣4或b>4D.4<b<
<b<﹣4或b>4D.4<b<![]() 或b<﹣4
或b<﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
A. (x2500)(8+4×![]() )=5000 B. (2900x2500)(8+4×
)=5000 B. (2900x2500)(8+4×![]() )=5000
)=5000
C. (x2500)(8+4×![]() )=5000 D. (2900x)(8+4×
)=5000 D. (2900x)(8+4×![]() )=5000
)=5000
查看答案和解析>>
科目:初中数学 来源: 题型:
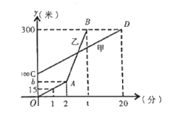
【题目】甲乙两人同时登同一座山,甲乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙在提速前登山的速度是______米/分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 __________米.
为 __________米.
(2)若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后![]() 和
和![]() 之间的函数关系式.
之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时甲距![]() 地的高度为多少米?
地的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() 在
在![]() 的左侧).
的左侧).
(1)求点![]() 的坐标及抛物线的对称轴;
的坐标及抛物线的对称轴;
(2)已知点![]() ,若抛物线与线段
,若抛物线与线段![]() 有公共点,请结合函数图象,求
有公共点,请结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
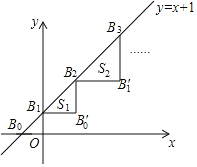
【题目】如图,直线y=x+1与x轴和y轴分别交于B0,B1两点,将B1B0绕B1逆时针旋转135°得B1B0′,过点B0'作y轴平行线,交直线y=x+1于点B2,记△B1B0B2的面积为S1;再将B2B1绕B2逆时针旋转135°得B2B1',过点B1'作y轴平行线,交直线y=x+l于点B3,记△B2B1'B3的面积为S2…以此类推,则△BnBn﹣1'Bn+1的面积为Sn=( )
A.(![]() )nB.(
)nB.(![]() )n﹣1C.2nD.2n﹣1
)n﹣1C.2nD.2n﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com