
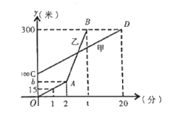
【题目】甲乙两人同时登同一座山,甲乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙在提速前登山的速度是______米/分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 __________米.
为 __________米.
(2)若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后![]() 和
和![]() 之间的函数关系式.
之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时甲距![]() 地的高度为多少米?
地的高度为多少米?
【答案】(1)15,30;(2)![]() ;(3)登山6.5分钟,乙追上了甲,此时甲距C地的高度为65米
;(3)登山6.5分钟,乙追上了甲,此时甲距C地的高度为65米
【解析】
(1)根据1分钟的路程是15米求出速度;用速度乘以时间得到此时的高度b;
(2)先求出t,设乙提速后的函数关系式为:![]() ,将
,将![]() 即可得到解析式;
即可得到解析式;
(3)先求出甲的函数解析式,再解甲乙的函数解析式组成的方程组求出交点的坐标,即可得到答案.
(1)乙在提速前登山的速度是![]() 15(米/分钟),乙在
15(米/分钟),乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为
为![]() 30 (米);
30 (米);
(2)t=20-9=11,
设乙提速后的函数关系式为:![]() ,图象经过
,图象经过![]()
![]()
则![]()
解得:![]()
所以乙提速后的关系式:![]() .
.
(3)设甲的函数关系式为:![]() ,将点
,将点![]() 和点
和点![]() 代入,则
代入,则 ![]() ,
,
解得:![]()
甲的函数关系式为:![]() ; 由题意得:
; 由题意得:
![]()
解得:![]() ,
,
相遇时甲距![]() 地的高度为:
地的高度为:![]() span>(米)
span>(米)
答:登山6.5分钟,乙追上了甲,此时甲距C地的高度为65米.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
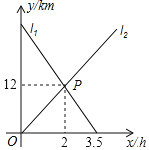
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l、l分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系.
(1)求这两条直线的解析式;
(2)当x为什么值时,小敏和小聪两人相距14km?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
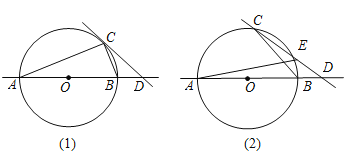
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E,BD:DE:EC=2;3:5求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现在C,D,E三点中,其中一点是另两点连线的中点的情况,问这样的情况出现几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
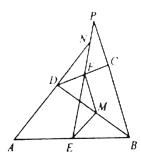
【题目】(习题再现)课本中有这样一道题目:如图,在四边形![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() .求证:
.求证:![]() .(不用证明)
.(不用证明)
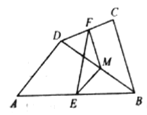
(习题变式)(1)如图,在“习题再现”的条件下,延长![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() .
.
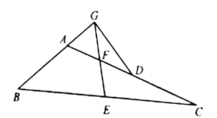
(2)如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字1、2、3的三张硬纸片,反面一样,现把三张硬纸片搅均反面朝上
(1)随机抽取一张,恰好是奇数的概率是多少
(2)先抽取一张作为十位数(不放回),再抽取一张作为个位数,能组成哪些两位数,将它们全部列出来,并求所取两位数大于20的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,每题10分,八年级(三)班的问卷得分情况统计图如下图所示:
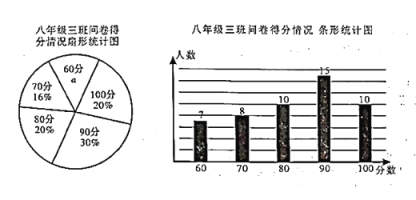
(1)扇形统计图中,a的值为 ________.
(2)根据以上统计图中的信息,求这问卷得分的众数和中位数分别是多少分?
(3)已知该校八年级共有学生600人,请估计问卷得分在80分以上(含80分)的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
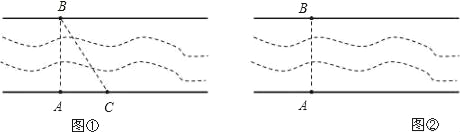
【题目】经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
(1)求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
(2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.(不用考虑计算问题,叙述清楚即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱护环境越来越受到社会各界的重视,为了让学生了解环保知识,某中学组织全校![]() 名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分
名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分![]() 分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
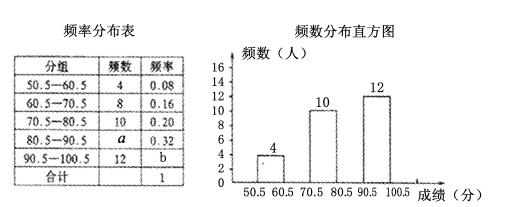
请根据以上的统计图、表解答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)成绩在![]() 分以上(不含
分以上(不含![]() 分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com