
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l、l分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系.
(1)求这两条直线的解析式;
(2)当x为什么值时,小敏和小聪两人相距14km?请说明理由.
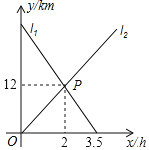
【答案】(1)y1=﹣8x+28,y2=6x;(2)当x=1h或x=3h时,小敏、小聪两人相距14km,见解析
【解析】
(1)设直线l1的函数表达式为y1=k1x+b(k1≠0),直线l2的函数表达式为y2=nx(n≠0),根据图象找出点的坐标,再利用待定系数法求出函数解析式即可得出结论;
(2)根据小聪和小敏两人相距14km结合两函数表达式即可得出关于x的含绝对值符号的一元一次方程,解方程即可得出结论.
解:(1)依题意 设直线l1的解析式为y1=k1x+b1,
将点(2,12),(3.5,0)代入,
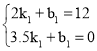 ,
,
解得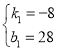 ,
,
则直线l1的解析式为y1=﹣8x+28.
设直线l2的解析式为y2=nx,
将点(2,12)代入,
得12=2n,
解得n=6,
则直线l2的解析式为y2=6x.
(2)∵小敏、小聪两人相距14km,
∴|y1﹣y2|=14,
∴|﹣8x+28﹣6x|=14,
∴28﹣14x=14或28﹣14x=﹣14,
解得x=1或x=3.
所以当x=1h或x=3h时,小敏、小聪两人相距14km.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
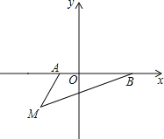
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a=_____,b=_____;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
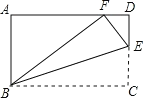
A. 2 B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
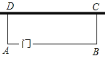
【题目】如图,现有![]() 长的篱笆,要围一个面积为
长的篱笆,要围一个面积为![]() 的花圃,花圃的一边靠墙(墙长
的花圃,花圃的一边靠墙(墙长![]() ),并在与墙平行的一边
),并在与墙平行的一边![]() 另外安装一道
另外安装一道![]() 宽的木门,那么花圃
宽的木门,那么花圃![]() 边的长为________
边的长为________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数值随自变量增大而增大 B. 函数图像与![]() 轴正方向成45°角
轴正方向成45°角
C. 函数图像不经过第四象限 D. 函数图像与![]() 轴交点坐标是(0,6)
轴交点坐标是(0,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
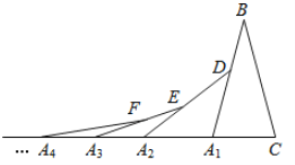
【题目】如图,在第1个![]() 中,
中,![]() ,
,![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第2个
,得到第2个![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .得到第3个
.得到第3个![]() ...按此做法继续下去,则第
...按此做法继续下去,则第![]() 个三角形中以
个三角形中以![]() 为顶点的内角度数是( )
为顶点的内角度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PEEQ的值是( )
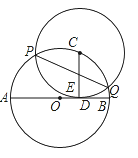
A. 24 B. 9 C. 36 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
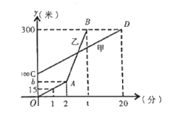
【题目】甲乙两人同时登同一座山,甲乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙在提速前登山的速度是______米/分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 __________米.
为 __________米.
(2)若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后![]() 和
和![]() 之间的函数关系式.
之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时甲距![]() 地的高度为多少米?
地的高度为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com