
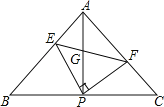
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
①∠B=∠C=45°;
②AE=CF,
③AP=EF,
④△EPF是等腰直角三角形,
⑤四边形AEPF的面积是△ABC面积的一半.
其中正确的结论是( )
A.只有① B.①②④ C.①②③④ D.①②④⑤
【答案】D
【解析】
试题分析:根据等腰直角三角形的性质得:∠B=∠C=45°,AP⊥BC,AP=![]() BC,AP平分∠BAC.所以可证∠C=∠EAP;∠FPC=∠EPA;AP=PC.即证得△APE与△CPF全等.根据全等三角形性质判断结论是否正确,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半.
BC,AP平分∠BAC.所以可证∠C=∠EAP;∠FPC=∠EPA;AP=PC.即证得△APE与△CPF全等.根据全等三角形性质判断结论是否正确,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半.
解:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴①∠B=∠C=![]() ×(180°﹣90°)=45°,AP⊥BC,AP=
×(180°﹣90°)=45°,AP⊥BC,AP=![]() BC=PC,∠BAP=∠CAP=45°=∠C,
BC=PC,∠BAP=∠CAP=45°=∠C,
∵∠APF+∠FPC=90°,∠APF+∠APE=90°,
∴∠FPC=∠EPA.
∴△APE≌△CPF(ASA),
∴②AE=CF;④EP=PF,即△EPF是等腰直角三角形;同理可证得△APF≌△BPE,
∴⑤四边形AEPF的面积是△ABC面积的一半,
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=![]() BC,
BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故③错误;
④∵∠AGF=∠EGP=180°﹣∠APE﹣∠PEF=180°﹣∠APE﹣45°,
∠AEP=180°﹣∠APE﹣∠EAP=180°﹣∠APE﹣45°,
∴∠AEP=∠AGF.
故正确的有①、②、④、⑤,共四个.
因此选D.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.

(1)当点D在线段BC上,∠NDB为锐角时,如图①,
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;
当点D在线段CB的延长线上,∠NDB为钝角时,如图③;
请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4![]() ,直接写出BE和CD的长度.
,直接写出BE和CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个三角形中,若一条边等于另一条边的两倍,则称这种三角形为“倍边三角形”. 例如:边长为a=2,b=3,c=4的三角形就是一个倍边三角形.
(1)如果一个倍边三角形的两边长为6和8,那么第三条边长所有可能的值为 .
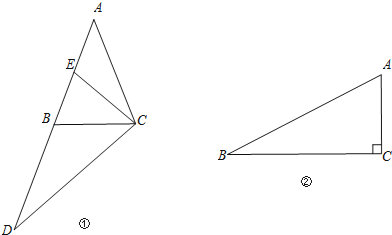
(2)如图①,在△ABC中,AB=AC,延长AB到D,使BD=AB,E是AB的中点.
求证:△DCE是倍边三角形;
(3)如图②,Rt△ABC中,∠C=90°,AC=4,BC=8,若点D在边AB上(点D不与A、B重合),且△BCD是倍边三角形,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com