
【题目】在一个三角形中,若一条边等于另一条边的两倍,则称这种三角形为“倍边三角形”. 例如:边长为a=2,b=3,c=4的三角形就是一个倍边三角形.
(1)如果一个倍边三角形的两边长为6和8,那么第三条边长所有可能的值为 .
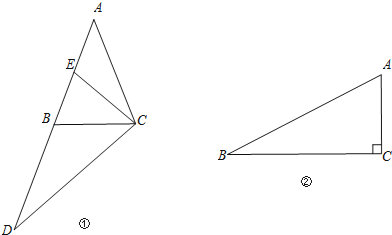
(2)如图①,在△ABC中,AB=AC,延长AB到D,使BD=AB,E是AB的中点.
求证:△DCE是倍边三角形;
(3)如图②,Rt△ABC中,∠C=90°,AC=4,BC=8,若点D在边AB上(点D不与A、B重合),且△BCD是倍边三角形,求BD的长.
【答案】(1)3,4,12;(2)见解析;(3)BD=4或![]() 或
或![]()
![]() 或
或![]() .
.
【解析】
试题分析:(1)直接利用倍边三角形的定义求解即可求得答案,注意三角形的三边关系;
(2)由已知,易证得△ACD∽△AEC,然后由相似三角形的对应边成比例,证得CD=2CE,即可证得结论;
(3)分BC=2BD、BC=2CD、BD=2CD、CD=2BD四种情况进行解答,求出各种情况下BD的长.
(1)解:∵一个倍边三角形的两边长为6和8,
∴第三边可能为:3,4,12,16,
∵6+8<16,不能组成三角形,舍去,
∴第三边可能为:3,4,12;
故答案为:3,4,12;
(2)证明:∵BD=AB=AC,
∴AD=2AC.即![]() =2.
=2.
∵E是AB的中点,
∴AB=2AE.
∴AC=2AE.即![]() =2,
=2,
∴![]() =
=![]() .
.
又∵∠A=∠A,
∴△ACD∽△AEC.
∴![]() =2.
=2.
∴△DCE是倍边三角形.
(3)∵在Rt△ABC中,∠C=90°,AC=4,BC=8,
∴AB=![]() =4
=4![]() ,
,
①当BC=2BD时,BD=4;
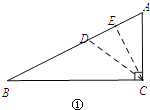
②当BC=2CD时,如图①,
CD=4,作CE⊥AB于E,
tanA=![]() =
=![]() =2,
=2,
设AE=x,则CE=2x,AC=![]() x,
x,
∴![]() x=4.x=
x=4.x=![]() .
.
∴AE=![]() ,
,
在△ACD中,CD=AC=4,CE⊥AB,
∴AD=2AE=![]() .
.
∴BD=AB﹣AD=![]() ;
;
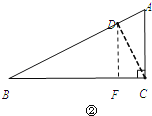
③当BD=2CD时,如图②,作DF⊥BC于F,
tanB=![]() =
=![]() =
=![]() ,
,
设DF=y,则BF=2y,BD=![]() y,
y,
∴CD=![]() y,CF=
y,CF=![]() y.
y.
∵BC=BF+CF,
∴8=2y+![]() y.
y.
解得y=![]() .
.
∴BD=![]()
![]() ;
;
④当CD=2BD时,如图③,过点D作DF⊥BC于F,
tanB=![]() =
=![]() =
=![]() ,
,
设DF=z,则BF=2z,BD=![]() z,
z,
∴CD=2![]() z,CF=
z,CF=![]() z.
z.
∵BC=BF+CF,
∴8=2z+![]() z.
z.
解得z=![]() ,
,
∴DF=![]() ,
,
∴BD=![]() ;
;
综上所述,BD=4或![]() 或
或![]()
![]() 或
或![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(.2016湖北随州第8题)随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8 B.28.8(1+x)2=20
C.20(1+x)2=28.8 D.20+20(1+x)+20(1+x)2=28.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.

(1)水果商要把水蜜桃售价至少定为多少才不会亏本?
(2)在销售过程中,根据市场调查与预测,水果商发现每天水蜜桃的销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示,那么当销售单价定为多少时,每天获得的利润是640元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
①∠B=∠C=45°;
②AE=CF,
③AP=EF,
④△EPF是等腰直角三角形,
⑤四边形AEPF的面积是△ABC面积的一半.
其中正确的结论是( )
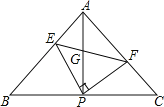
A.只有① B.①②④ C.①②③④ D.①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.

(1)求证:DE=DC;
(2)求证:直线DC是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com