
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用代入消元法求出解即可;
(4)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+3y=4①}\\{2x-3y=-1②}\end{array}\right.$,
①+②得:3x=3,即x=1,
把x=1代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{4x-3y=5①}\\{4x+6y=14②}\end{array}\right.$,
②-①得:9y=9,即y=1,
把y=1代入①得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{x=6①}\\{-x+9y=2②}\end{array}\right.$,
把①代入②得:-6+9y=2,即y=$\frac{8}{9}$,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=\frac{8}{9}}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{23x+17y=63①}\\{17x+23y=57②}\end{array}\right.$,
①+②得:40(x+y)=120,即x+y=3③,
③×23-①得:6y=6,即y=1,
把y=1代入③得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (-x-2)(x-2)=x2-4 | B. | 2x(x2-2x-3)=2x3-4x2-6x | ||
| C. | (x-2y)2=x2-4xy+2y2 | D. | (x-1)(x+4)=x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
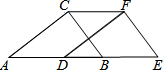 如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,BM是∠ABC的平分线,交CD于点M,且DM=2,平行四边形ABCD的周长是14,则BC的长等于( )
如图,在平行四边形ABCD中,BM是∠ABC的平分线,交CD于点M,且DM=2,平行四边形ABCD的周长是14,则BC的长等于( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p=-5,q=6 | B. | p=1,q=-6 | C. | p=1,q=6 | D. | p=-1,q=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠ABD和∠BDC两个角的平分线交于点E,DE的延长线交AB于F.
如图,∠ABD和∠BDC两个角的平分线交于点E,DE的延长线交AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com