Question

已知直线l₁、l₂的函数关系式分别为y=-

4

3

x+7，y=-x+b；直线l₂与x轴的交点为A，与y轴的交点为B，
（1）求∠BAO的度数；
（2）若将坐标原点O沿直线l₂翻折到直线l₁上，记为点C，求点C的坐标；
（3）在（2）的情形下，求直线l₁、l₂及x轴、y轴所围成的图形面积．

Answer 1

考点：一次函数图象与几何变换,两条直线相交或平行问题

专题：

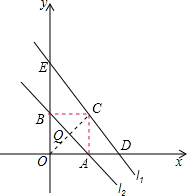
分析：（1）先由直线l₂的解析式y=-x+b，分别求出直线l₂与x轴的交点A，与y轴的交点B的坐标，进而得到求∠BAO的度数；
（2）设C的坐标（c，d），然后根据直线l₂是线段OC的垂直平分线，得到斜率乘积为-1且C点在直线l₁上，分别列出两个关于c与d的方程，联立两个方程即可求出c与d的值，得到C的坐标；
（3）将OC的中点Q（

3

2

，

3

2

）代入直线直线y=-x+b，求得b的值，代入直线l₂的函数关系式求得点A、B的坐标．所以所求图形的面积=△EOD的面积-△BOA的面积．

解答：解：（1）∵y=-x+b，
∴当y=0时，-x+b=0，解得x=b，
当x=0时，y=b，
∴A（b，0），B（0，b），
∴OA=OB，
∴△AOB为等腰直角三角形，
∴∠BAO=45°；

（2）设C（c，d），直线y=-x+b的斜率k=-1，
∵直线OC与直线y=-x+b垂直，
∴k_OC=1=

d

c

，即c=d①；
又∵C点在直线l₁上，
代入直线y=-

4

3

x+7得：d=-

4

3

c+7②，
联立①②解得：c=3，d=3，
∴点C的坐标为（3，3）；

（3）∵OC的中点Q在直线y=-x+b上，Q（

3

2

，

3

2

），代入直线直线y=-x+b得，

3

2

=-

3

2

+b，
解得b=3，
∴A（3，0），B（0，3），
S_△BOA=

1

2

OA•OB=

1

2

×3×3=

9

2

，
则易求D（

21

4

，0），E（0，7），
∴S_△EOD=

1

2

OE•OD=

1

2

×7×

21

4

=

147

8

，
∴直线l₁、l₂及x轴、y轴所围成的图形面积，即S_{四边形ABCD}=S_△EOD-S_△BOA=

147

8

-

9

2

=

111

8

．

点评：本题考查了一次函数图象与几何变换，运用待定系数法求一次函数解析式，坐标与图形的性质以及轴对称图形的性质．难度较大，需要学生掌握一定的综合知识．