
【题目】如图所示,点A、E、F、C在同一直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,且AB=CD,
(1)AB与CD平行吗?若平行请说明理由;
(2)证明BD平分EF.
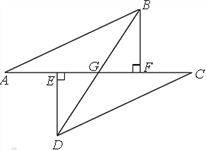
【答案】(1)AB与CD平行,证明见解析;(2)证明见解析.
【解析】试题分析:(1)由AE=CF,可得AF=CE,再由DE⊥AC,BF⊥AC,AB=CD,推出Rt△BFA和Rt△DEC全等,根据全等三角形的性质,即可推出BF=DE,∠A=∠C,由内错角相等两直线平行即可推出结论,(2)由AAS证出△BFG和△DEG全等,再由全等三角形的性质得出EG=FG即可得证.
试题解析:(1)AB与CD平行,理由如下:
∵AE=CF,
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°,
∵在Rt△BFA和Rt△DEC中, ![]()
∴Rt△BFA≌Rt△DEC(HL),
∴BF=DE,∠A=∠C,
∴AB∥CD.
(2)在△BFG和△DEG中, 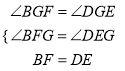
∴△BFG≌△DEG(AAS),
∴EG=FG,
∴BD平分EF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】地球的平均半径约为637100米,该数字用科学记数法可表示为( )
A.6371×103
B.0.6371×107
C.6.371×105
D.6.371×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人连续7年调查某县养鸡业的情况,提供了如下两方面的信息图:

甲调查表明:养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只;
乙调查表明:养鸡场的个数由第1年的46个减少到第7年的22个.
现在给出下列四个判断:(1)该县第2年养鸡场产鸡的数量为1.3万只;(2)该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量;(3)该县这7年养鸡场产鸡的数量逐年增长;(4)在这7年中,第5年该县养鸡场产鸡的数量最多.
根据甲、乙两人提供的信息,可知其中正确的判断有( ).
A. 3个 B. 2个 C. 1 个 D. 0 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )

A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
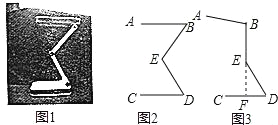
【题目】图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.
(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;
(2)为保护视力,写字时眼睛离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时∠ABE的最大值.(结果精确到0.01°,参考数据: ![]() ≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角△BCD绕点B旋转.
(1)如图1,当等腰直角△BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数.
(2)如图2,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角△BCD的直角边CD会与半圆O相切于点E?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com