
【题目】已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角△BCD绕点B旋转.
(1)如图1,当等腰直角△BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数.
(2)如图2,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角△BCD的直角边CD会与半圆O相切于点E?请说明理由.

【答案】(1)、110°;(2)、β=![]() α+45°
α+45°
【解析】
试题分析:(1)、连接OG、OH.由题意可知:∠AOG=20°,由等腰直角三角形的性质可求得∠CBD=45°,接下来,依据圆周角定理可求得∠HOG=90°,最后依据∠AOH=∠AOG+∠GOH求解即可;(2)、连接OG、OE.先由切线的性质证明OE⊥DC,然后依据平行线的判定定理可证明EO∥CB,接下来依据平行线的性质和可得到∠EOA=∠CBA,最后结合圆周角定理以及∠ABC、∠ABG、∠DBC的关系可得到α、β的关系.
试题解析:(1)、如图1所示:连接OG、OH.
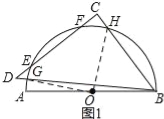
∵点G在量角器上的读数为20°, ∴∠AOG=20°. ∵△BCD为等腰直角三角形,
∴∠CBD=45°. ∴∠HOG=90°. ∴∠AOH=∠AOG+∠GOH=20°+90°=110°.
(2)、如图2所示:连接OG、OE.
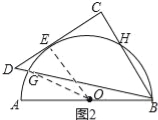
∵DC为圆O的切线,E为切点, ∴∠OED=90°. ∴∠OED=∠C. ∴EO∥CB.
∴∠EOA=∠CBA=β. 又∵∠GBA=![]() ∠GOA=
∠GOA=![]() α,∠ABC=∠ABG+∠DBC, ∴β=
α,∠ABC=∠ABG+∠DBC, ∴β=![]() α+45°.
α+45°.


科目:初中数学 来源: 题型:
【题目】近年来,某市旅游事业蓬勃发展,吸引大批海内外游客前来观光旅游.下面的两副图分别反映了该市从2003年到2006年游客总人数和旅游业总收入的情况:

根据统计图提供的信息,解答下列的问题:
(1)2006年游客总人数为__________万人次,旅游业总收入为_________万元;
(2)在2004、2005、2006年这三年中,旅游业总收入增长幅度最大的是________年,这一年的旅游业总收入比上一年增长的百分率为________(精确到0.1%);
(3)在2006年的游客中,国内游客为1200万人,其余为海外游客.据统计,国内游客的人均消费约为700元,海外游客的人均消费约为多少元?(注:旅游收入=游客人数×游客的人均消费)
查看答案和解析>>
科目:初中数学 来源: 题型:
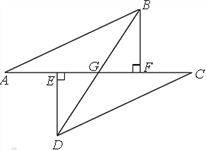
【题目】如图所示,点A、E、F、C在同一直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,且AB=CD,
(1)AB与CD平行吗?若平行请说明理由;
(2)证明BD平分EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”:用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,随机被甲、乙、丙三人抢到.
(1)以下说法中正确的是
A.甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多
B.甲一定抢到金额最多的红包
C.乙一定抢到金额居中的红包
D.丙不一定抢到金额最少的红包
(2)记金额最多、居中、最少的红包分别为A,B,C,试求出甲抢到红包A的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上的一点,∠B =40°,∠ADC=80°.
(1)求证:AD=BD;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳沙井某服装厂2017年销售额为8亿元,受中美贸易战影响,估计2019年销售额降为5.12亿元,设平均每年下降的百分比为x,可列方程为( )
A.8(1﹣x)=5.12B.8(1+x)2=5.12
C.8(1﹣x)2=5.12D.5.12(1+x)2=8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com