
【题目】如图,一次函数y=![]() 的图象与正比例函数y=mx(m≠0)的图象交于点A(a,2),与x轴交于点B.现将直线OA向右平移使其经过点B,平移后的直线与y轴交于点C,连接AC,则四边形AOBC的面积为_____.
的图象与正比例函数y=mx(m≠0)的图象交于点A(a,2),与x轴交于点B.现将直线OA向右平移使其经过点B,平移后的直线与y轴交于点C,连接AC,则四边形AOBC的面积为_____.
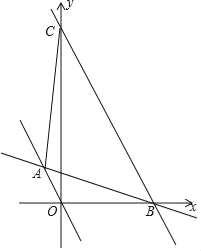
【答案】12
【解析】
把点A(a,2)代入y=![]() 得到a=﹣1,把A(﹣1,2)代入y=mx得到m=﹣2,即直线OA解析式为y=﹣2x,再求出B(3,0),设BC的解析式为y=﹣2x+b',把B(3,0)代入求得直线BC的解析式y=﹣2x+6,可得C(0,6),然后根据三角形的面积公式计算即可.
得到a=﹣1,把A(﹣1,2)代入y=mx得到m=﹣2,即直线OA解析式为y=﹣2x,再求出B(3,0),设BC的解析式为y=﹣2x+b',把B(3,0)代入求得直线BC的解析式y=﹣2x+6,可得C(0,6),然后根据三角形的面积公式计算即可.
解:把点A(a,2)代入y=![]() 得,a=﹣1,
得,a=﹣1,
∴A(﹣1,2),
把A(﹣1,2)代入y=mx得,m=﹣2,
∴直线OA解析式为:y=﹣2x,
令y=![]() =0,
=0,
解得:x=3,
∴B(3,0),
由平移可得,BC∥AO,
设BC的解析式为y=﹣2x+b',把B(3,0)代入,可得b'=6,
∴直线BC的解析式为:y=﹣2x+6,
令x=0,则y=6,即C(0,6),
∴OC=6,
∴四边形AOBC的面积=S△ACO+S△BCO=![]() ×6×1+
×6×1+![]() ×6×3=12.
×6×3=12.
故答案为:12.


科目:初中数学 来源: 题型:
【题目】由于化工原料对人体健康的影响,所以某运输公司采用![]() 、
、![]() 两种机器人搬运化工原料,已知
两种机器人搬运化工原料,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运
型机器人每小时多搬运![]() ,
,![]() 型机器人搬运
型机器人搬运![]() 所用时间与
所用时间与![]() 型机器人搬运
型机器人搬运![]() 所用时间相等.
所用时间相等.
(1)求这两种机器人每小时分别搬运多少化工原料;
(2)该公司要搬运一批共计![]() 的化工原料,由于场地限制,两种机器人不能同时工作,公司要求不超过10小时完成搬运任务,请你帮该公司计算一下
的化工原料,由于场地限制,两种机器人不能同时工作,公司要求不超过10小时完成搬运任务,请你帮该公司计算一下![]() 型机器人至少需要工作多少小时.
型机器人至少需要工作多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
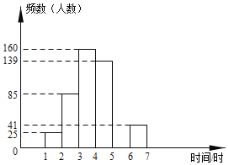
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】罚球是篮球比赛中得分的一个组成部分,罚球命中率的高低对篮球比赛的结果影响很大.如图是对某球员罚球训练时命中情况的统计:

下面三个推断:①当罚球次数是500时,该球员命中次数是411,所以“罚球命中”的概率是0.822;②随着罚球次数的增加,“罚球命中”的频率总在0.812附近摆动,显示出一定的稳定性,可以估计该球员“罚球命中”的概率是0.812;③由于该球员“罚球命中”的频率的平均值是0.809,所以“罚球命中”的概率是0.809.其中合理的是( )
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.下面是小文的探究过程,请补充完整:
的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:

如图,在平面直角坐标系![]() 中,描出了以上表中各对应值为坐标的点.
中,描出了以上表中各对应值为坐标的点.
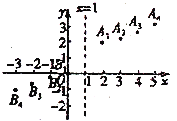
①观察图中各点的位置发现:点![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 均关于某点中心对称,则该点的坐标为__________;
均关于某点中心对称,则该点的坐标为__________;
②小文分析函数![]() 表达式发现:当
表达式发现:当![]() 时,该函数的最大值为0,则该函数图象在直线
时,该函数的最大值为0,则该函数图象在直线![]() 左侧的最高点的坐标为__________;
左侧的最高点的坐标为__________;
(3)小文补充了该函数图象上两个点![]() ,
,![]() .
.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
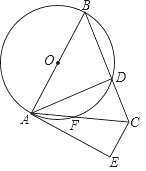
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=10,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com