
����Ŀ�����ڻ���ԭ�϶����彡����Ӱ�죬����ij���乫˾����![]() ��
��![]() ���ֻ����˰��˻���ԭ�ϣ���֪
���ֻ����˰��˻���ԭ�ϣ���֪![]() �ͻ����˱�
�ͻ����˱�![]() �ͻ�����ÿСʱ�����
�ͻ�����ÿСʱ�����![]() ��
��![]() �ͻ����˰���
�ͻ����˰���![]() ����ʱ����
����ʱ����![]() �ͻ����˰���
�ͻ����˰���![]() ����ʱ�����.
����ʱ�����.
��1���������ֻ�����ÿСʱ�ֱ���˶��ٻ���ԭ�ϣ�
��2���ù�˾Ҫ����һ������![]() �Ļ���ԭ�ϣ����ڳ������ƣ����ֻ����˲���ͬʱ��������˾Ҫ����10Сʱ��ɰ������������ù�˾����һ��
�Ļ���ԭ�ϣ����ڳ������ƣ����ֻ����˲���ͬʱ��������˾Ҫ����10Сʱ��ɰ������������ù�˾����һ��![]() �ͻ�����������Ҫ��������Сʱ.
�ͻ�����������Ҫ��������Сʱ.
���𰸡���1��![]() �ͻ�����ÿСʱ����
�ͻ�����ÿСʱ����![]() ��
��![]() �ͻ�����ÿСʱ����
�ͻ�����ÿСʱ����![]() ����2��
����2��![]() �ͻ��������ٹ���6Сʱ.
�ͻ��������ٹ���6Сʱ.
��������
��1����B�ͻ�����ÿСʱ����xkg����ԭ�ϣ���A�ͻ�����ÿСʱ���ˣ�x+30��kg����ԭ�ϣ�����A�ͻ����˰���900kgԭ������ʱ����B�ͻ����˰���600kgԭ������ʱ����ȣ����ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2����A�ͻ����˹���yСʱ��������������ԭ�ϲ�����10Сʱȫ����������г�����ʽ�����
��1����![]() �ͻ�����ÿСʱ����
�ͻ�����ÿСʱ����![]() ����
����![]() �ͻ�����ÿСʱ����
�ͻ�����ÿСʱ����![]() ��
��
�����⣬��![]() ��
��
���x=60��
������x=60��ԭ���̵Ľ⣬�ҷ������⣬
����x+30=90��
��B�ͻ�����ÿСʱ����60kg����A�ͻ�����ÿСʱ����90kg��
��2����![]() �ͻ����˹���
�ͻ����˹���![]() Сʱ��
Сʱ��
�в���ʽ��![]() ��
��
��ã�![]() .
.
��![]() �ͻ��������ٹ���6Сʱ.
�ͻ��������ٹ���6Сʱ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ͬһ��·��˳������������A��B��C���ס��������οʹӾ���A�������ײ��е�����C���һ�20����ʱ���ŶӺ�˹۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ס��������뾰��A��·��s���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��
��1�����ٶ��� ��/���ӣ�
��2����20��t ��30ʱ�������뾰��A��·��s��t�ĺ�������ʽ��
��3���ҳ�����ʱ�������;��������
��4���������ᄚ��Cʱ�����뾰��C��·��Ϊ360�ף����ҴӾ���B���е�����C���ٶ��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���������ֱ�����������¶��壺
��P��x��m����ͼ��G1�ϵ�����һ�㣬��Q��x��n����ͼ��G2�ϵ�����һ�㣬������ֱ��l��kx+b��k��0������m��kx+b��n��kx+b�����ֱ��l��y=kx+b��k��0����ͼ��G1��G2��������ֱ������
��ͼ��ֱ��l��y=-x-4�Ǻ���y=![]() ��x��0����ͼ����������OABC��һ��������ֱ������
��x��0����ͼ����������OABC��һ��������ֱ������
��1����ֱ��y1=-2x��y2=3x+1��y3=-x+3�У�����ͼ����y=![]() ��x��0����ͼ����������OABC��������ֱ������Ϊy1=-2x��
��x��0����ͼ����������OABC��������ֱ������Ϊy1=-2x��
������д��һ����������IJ�ͬ��������ֱ�����ı���ʽ��y=-3x��
��2����ͼ����һ���ĵ���ֱ��������EDF�������ֱ���������ƽ�У�ֱ�Ƕ���D�������ǣ�![]() ��1������O�İ뾶Ϊ2���Ƿ������EDF���O��������ֱ�����������ڣ������������ֱ�����ı���ʽ���������ڣ���˵�����ɣ�
��1������O�İ뾶Ϊ2���Ƿ������EDF���O��������ֱ�����������ڣ������������ֱ�����ı���ʽ���������ڣ���˵�����ɣ�
��3��������A1B1C1D1��һ����y���ϣ��������߶���y����Ҳ࣬��M��1��t���Ǵ������ε����ģ�������ֱ��y=2x+b�Ǻ���y=x2-2x-3��0��x��4����ͼ����������A1B1C1D1��������ֱ��������ֱ��д��t��ȡֵ��Χ��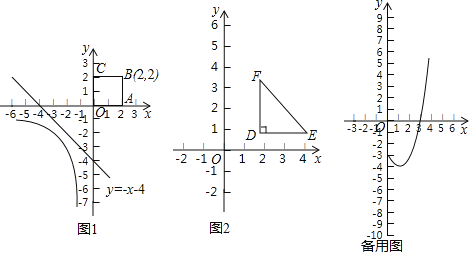
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
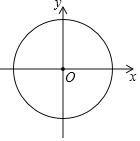
����Ŀ����ƽ��ֱ������ϵxOy�У�![]() �İ뾶��5����AΪ
�İ뾶��5����AΪ![]() ��һ�㣬
��һ�㣬![]() ���ڵ�
���ڵ�![]() ���ڵ�C�����ı���ABOC�����Ϊ12��д��һ�����������ĵ�A������______��
���ڵ�C�����ı���ABOC�����Ϊ12��д��һ�����������ĵ�A������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
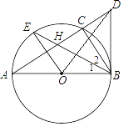
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬����B����O�����ߣ���AC�ӳ��߽��ڵ�D������BC��OE//BC����O�ڵ�E������BE��AC�ڵ�H����1����֤��BEƽ�֡�ABC����2������OD����BH=BD=2����OD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У�������![]() ������A(0��-3)��B(4��5).
������A(0��-3)��B(4��5).
��1����������߱���ʽ������M�����ꣻ
��2�����M����y��ĶԳƵ���N������������A��B����֮��IJ��ּ�Ϊͼ��W(����A,B����)��������N��ֱ��l�� ![]() ��ͼ��Wǡһ���й����㣬���ͼ����m��ȡֵ��Χ.
��ͼ��Wǡһ���й����㣬���ͼ����m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�����⣺̽������![]() ��ͼ������ʣ�С�¸���ѧϰ�����ľ��飬�Ժ���
��ͼ������ʣ�С�¸���ѧϰ�����ľ��飬�Ժ���![]() ��ͼ������ʽ�����̽����������С�µ�̽�����̣��벹��������
��ͼ������ʽ�����̽����������С�µ�̽�����̣��벹��������
x | �� |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | �� |
y | �� |
|
|
|
|
|
|
|
| 2 | m |
|
| �� |
��1������![]() ���Ա���x��ȡֵ��Χ��___________��
���Ա���x��ȡֵ��Χ��___________��
��2���±���y��x�ļ����Ӧֵ����m��ֵ��
��3����ͼ����ƽ��ֱ������ϵ![]() �У���������ϱ��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ��
�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ��
��4����һ��̽�����֣��ú���ͼ���ڵ�һ�����ڵ���͵�������ǣ�2��2������Ϻ���ͼ��д���ú������������ʣ�һ�����ɣ���______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ������̽��ͼ���н�֮��ĵ�����ϵ��������⣮
�����龳��
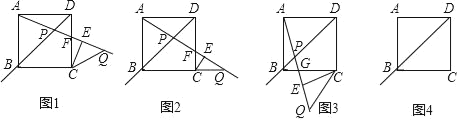
������ABCD�У���P������DB�ϵ�һ�����㣬����C��CE��AP�ڵ�E����Q���P���ڵ�E�Գƣ�����CQ�����DAP����(0�㣼����135��)����QCE������
����̽����
(1)��ͼ1��Ϊ̽���������Ĺ�ϵ����˼С���ͬѧ������0�㣼����45��ʱ�����Σ�����AP���CD���ڵ�F�����ǵó���ʱ�������Ĺ�ϵ������2����������һ���ۿɵõ���Qǡ�������߶�BC���ӳ�����(��ͼ2)ʱ�������� ���㣬������ ���㣻
����̽����
(2)��ѧС���ͬѧ����45�㣼����90��ʱ��ͼ����ͼ3������AP���BC���ڵ�G��������ʱ������֮��ĵ�����ϵ����֤�����ۣ�
��չ���죺
(3)�������ͼ4��һ��̽��������90�㣼����135��ʱ��������֮��ĵ�����ϵΪ�� ����
����֪�����α߳�Ϊ2���ڵ�P�˶������У���������ʱ��PQ�ij�Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
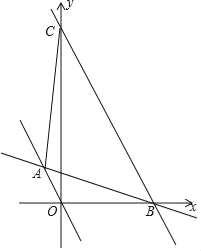
����Ŀ����ͼ��һ�κ���y��![]() ��ͼ��������������y��mx��m��0����ͼ���ڵ�A��a��2������x�ύ�ڵ�B���ֽ�ֱ��OA����ƽ��ʹ�侭����B��ƽ�ƺ��ֱ����y�ύ�ڵ�C������AC�����ı���AOBC�����Ϊ_____��
��ͼ��������������y��mx��m��0����ͼ���ڵ�A��a��2������x�ύ�ڵ�B���ֽ�ֱ��OA����ƽ��ʹ�侭����B��ƽ�ƺ��ֱ����y�ύ�ڵ�C������AC�����ı���AOBC�����Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com