
【题目】已知二次函数y=2x2+bx﹣1(b为常数).
(1)若抛物线经过点(1,2b),求b的值;
(2)求证:无论b取何值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点;
(3)若平行于x轴的直线与该二次函数的图象交于点A,B,且点A,B的横坐标之和大于1,求b的取值范围.
【答案】(1)b=1;(2)见解析;(3)b<﹣2.
【解析】
(1)把点(1,2b)代入抛物线解析式即可得解;
(2)计算判别式的值得到△=b2+8,利用非负数的性质得到△>0,然后根据判别式的意义得到结论;
(3)将平行于x轴的直线y=m与抛物线联立得出关于x的方程,由其交点的横坐标之和大于1可得出有关b的不等式,即可求解.
解:(1)把点P(1,2b)代入抛物线y=2x2+bx﹣1中,得
2+b﹣1=2b,
解得:b=1.
(2)证明:∵△=b2﹣4×2×(﹣1)=b2+8,
∵无论b取何值,b2≥0,
∴b2+8>0,
∴二次函数y=2x2+b x﹣1图象与x轴必有两个交点.
(3)设平行于x轴的直线为y=m,
∵直线y=m与该二次函数的图象交于点A,B,
∴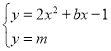 ,
,
整理得,2x2+bx﹣1﹣m=0,
若x1,x2是方程2x2+bx﹣1﹣m=0的两根,则x1,x2是直线与抛物线交点A,B的横坐标,
∴![]() ,
,
由题意得,![]() ,解得,b<﹣2.
,解得,b<﹣2.
∴b的取值范围是b<﹣2.


科目:初中数学 来源: 题型:
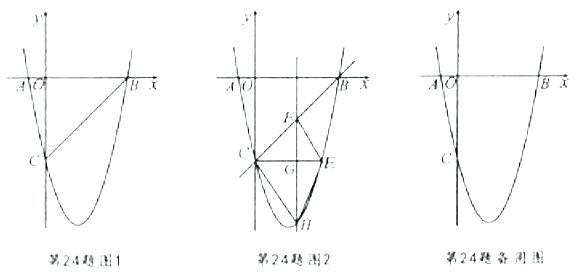
【题目】如图1,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 是
是![]() 轴上的一点,且以
轴上的一点,且以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 轴玮抛物线相交于点
轴玮抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,试探究当点
,试探究当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 的面积最大,求点
的面积最大,求点![]() 的坐标及最大面积;
的坐标及最大面积;
(4)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴,
轴,![]() 轴上分别找点
轴上分别找点![]() ,
,![]() ,使四边形
,使四边形![]() 的周长最小,求出点
的周长最小,求出点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
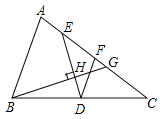
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了为期一周的“敬老爱亲”社会活动,为了解情况,学生会随机调查了部分学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组,A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).

请根据图中提供的信息,解答下列问题:
(1)学生会随机调查了 名学生;
(2)补全频数分布直方图;
(3)若全校有900名学生,估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
![]() ______,
______,![]() ______.
______.
![]() 该调查统计数据的中位数是______,众数是______.
该调查统计数据的中位数是______,众数是______.
![]() 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
![]() 若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
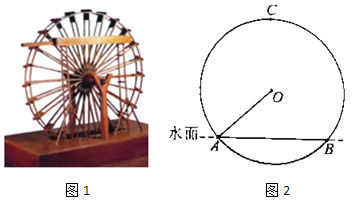
【题目】筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )
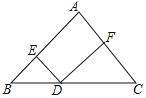
A. 34B. 32C. 22D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.
(1) 求证:DE⊥AC;
(2) 连结OC交DE于点F,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com