
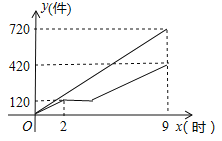
����Ŀ���ס���������ͬʱ��ʼ�ӹ�һ����װ���ӎ�ʼ�ӹ����ӹ���������װ�׳��乤����9Сʱ���ҳ�������;ͣ��һ��ʱ��ά���豸��Ȼ��ͣ��ǰ�Ĺ���Ч�ʼ����ӹ���ֱ����׳���ͬʱ���������װ�ļӹ�����Ϊֹ����ס�����������Լӹ���װ������Ϊy���������׳���ӹ���ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ��
��1���׳���ÿСʱ�ӹ���װ����Ϊ ����������װ���ܼ���Ϊ ����
��2�����ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽ��
��3����ס��������乲ͬ�ӹ���1000����װʱ�׳������õ�ʱ�䣮
���𰸡���1��80��1140����2��y=60x��120��4��x��9������3��8��
��������
������1�����ݹ���Ч��=��������������ʱ�䣬��������׳���ÿСʱ�ӹ���װ�������ٸ���������װ���ܼ���=�׳���ӹ��ļ���+�ҳ���ӹ��ļ������������������װ���ܼ�����
��2�����ݹ���Ч��=��������������ʱ�䣬��������ҳ���ÿСʱ�ӹ���װ���������ݹ���ʱ��=��������������Ч�ʽ�Ϲ�������ʱ�䣬��������ҳ������豸ʱ�䣬�ٸ��ݼӹ��ķ�װ�ܼ���=120+����Ч��������ʱ�䣬��������ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽ��
��3�����ݼӹ��ķ�װ�ܼ���=����Ч��������ʱ�䣬����׳���ӹ���װ����y��x֮��ĺ�����ϵʽ�����ס�������ϵʽ����������1000�����xֵ������ý⣮
����������⣺��1���׳���ÿСʱ�ӹ���װ����Ϊ720��9=80��������������װ���ܼ���Ϊ720+420=1140��������
�ʴ�Ϊ��80��1140��
��2���ҳ���ÿСʱ�ӹ���װ����Ϊ120��2=60���������ҳ������豸��ʱ��Ϊ9����420��120����60=4��ʱ�������ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽΪy=120+60��x��4��=60x��120��4��x��9����
��3���׳���ӹ���װ����y��x֮��ĺ�����ϵʽΪy=80x����80x+60x��120=1000ʱ��x=8��
�𣺼ס��������乲ͬ�ӹ���1000����װʱ�׳������õ�ʱ��Ϊ8Сʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ĵ�λ����Ϊ1��
![]()
��1�������B��D��ʾ������Ϊ�෴������ôͼ�е�A����D��ʾ�����ֱ��� �� ��
��2������BΪԭ��ʱ�����������Ƿ���ڵ�M��ʹ�õ�M����A�ľ����ǵ�M����D�ľ����2���������ڣ��������ʱ��M����ʾ�������������ڣ�˵�����ɣ�
��3�� �ڣ�2���������£���A����C�ֱ���2����λ����/���0.5����λ����ͬʱ�����˶���ͬʱ��P��ԭ�������3����λ����/����ٶ������˶�������A���C֮��ľ���Ϊ3����λ����ʱ�����P����Ӧ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+m��ͼ���y�ύ�ڵ�B��������������y=![]() xͼ���ڵ�P��2��n����
xͼ���ڵ�P��2��n����
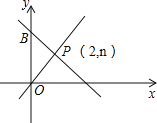
��1����m��n��ֵ��
��2������POB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,һ�κӰӵĶ���Ϊ����ABCD,�Ը���ͼ������,����½�![]() �Ͱӵ�AD.������������ţ�
�Ͱӵ�AD.������������ţ�
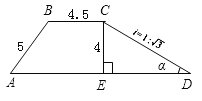
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУһ����İ����δ���ð�����ϳ���ѧ����ȥ���Σ���������˵���������ʦ����ȫƱ����ôѧ��Ʊ����5���Ż�������������˵����������ʦƱ����ȫ����Ʊ�۵�6���Ż���.����ȫƱƱ��Ϊ240Ԫ/��.
��1������![]() ��ѧ������д����.������������ķ��õĴ���ʽ.
��ѧ������д����.������������ķ��õĴ���ʽ.
��2������10��ѧ���μӣ������ĸ�������ʡǮ?��˵������.4��ѧ���أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
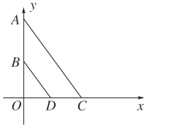
����Ŀ����ͼ8����ƽ��ֱ������ϵxOy�У�A(0��8)��B(0��4)����C��x����������ϣ���DΪOC���е㣮
��1����BD��AC�ľ������2ʱ�����߶�OC�ij���
��2�����OE��AC�ڵ�E�����ı���ABDEΪƽ���ı���ʱ����ֱ��BD�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һƬ���������֣�����25�����ӣ�Ϊ�˷��������ÿ�����Ӷ����Լ��ı�ţ���ͼ��ʾ������2��3��5��7��10��13��17��21�����Ӷ��ڹսǴ������![]() ��Ҳ��һ�����ӣ����Ϊ26���ڴ�ת�䣨�����ߣ��������Ϲ��ɼ��������ӣ����200���սǴ����2�ڵ�1���սǴ��������ӵı��ӦΪ�� ��
��Ҳ��һ�����ӣ����Ϊ26���ڴ�ת�䣨�����ߣ��������Ϲ��ɼ��������ӣ����200���սǴ����2�ڵ�1���սǴ��������ӵı��ӦΪ�� ��

A.10010B.10101
C.10100D.10110
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪P����O��һ�㣬PO����O�ڵ�C��OC=CP=2����AB��OC����AOC�Ķ���Ϊ60�㣬����PB��
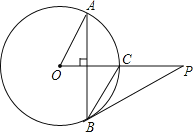
��1����BC�ij���
��2����֤��PB����O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
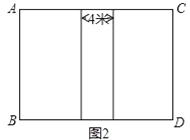
����Ŀ��ijУΪѧ����չ��չ�Կγ̣�����һ�鳤�ȿ���6�ij����γ����ڽ���������������ɵ�ֲ����ֳ������ͼ1����Ҫ����������֮���м��4��·����Ʒ�����ͼ2����֪ÿ��������ܳ�Ϊ44�ף�
��1����ÿ������ij��Ϳ����Ƕ��٣�
��2���������ִ�����۵ķ���������һ��ÿƽ����60Ԫ������100ƽ�����Ż�500Ԫ����������ÿƽ����70Ԫ������100ƽ�����Ż��ܼ۵�20%������ѡ�����ַ������Żݣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com