
����Ŀ��Сӱ��С������ͬѧ��ѧϰ��������ʱ���������ӣ��ʵؾ��ȵ������壩���顣
(1)Сӱ��С����ʵ�����������һö���ӣ���ô��ö���ӳ��ϵĵ���֮��Ϊ����ʱ�ĸ������?�����б�����״ͼ�ķ�������˵����������������ʡ�
(2)������һ��ʵ���й�������60�Σ�����Ľ�����£�
![]()
����գ��˴�ʵ������5�㳯������Ƶ��Ϊ______��
��С��˵��������ʵ�飬����5�㳯�ϵĸ������������˵����ȷ��?Ϊʲô?
���𰸡�(1)P(����֮��Ϊ7) =![]() ��(2)��
��(2)��![]() ����˵���Ǵ���ġ�����������У���5�㳯�ϡ���Ƶ�������˵����5�㳯�ϡ���һ�¼������ĸ��������Ϊ������Ĵ����ϴ�ʱ��Ƶ���ȶ��ڸ��ʣ���������ȫ���ڸ��ʡ�
����˵���Ǵ���ġ�����������У���5�㳯�ϡ���Ƶ�������˵����5�㳯�ϡ���һ�¼������ĸ��������Ϊ������Ĵ����ϴ�ʱ��Ƶ���ȶ��ڸ��ʣ���������ȫ���ڸ��ʡ�
��������
��1���оٳ�����������Ƚ���ö���ӳ��ϵĵ���֮�͵�������������������������������������ļ��ɣ�
��2������5���ֵĴ��������ܴ�����Ϊ�����Ƶ�ʣ��ڸ��ݸ��ʵ����壬��Ҫ����������У�
�⣺��1���б�����
��1��6�� | ��2��6�� | ��3��6�� | ��4��6�� | ��5��6�� | ��6��6�� |
��1��5�� | ��2��5�� | ��3��5�� | ��4��5�� | ��5��5�� | ��6��5�� |
��1��4�� | ��2��4�� | ��3��4�� | ��4��4�� | ��5��4�� | ��6��4�� |
��1��3�� | ��2��3�� | ��3��3�� | ��4��3�� | ��5��3�� | ��6��3�� |
��1��2�� | ��2��2�� | ��3��2�� | ��4��2�� | ��5��2�� | ��6��2�� |
��1��1�� | ��2��1�� | ��3��1�� | ��4��1�� | ��5��1�� | ��6��1�� |
�ɱ�����Կ��������������36�֣�֮��Ϊ7���������࣬Ϊ6�֣�
����P(����֮��Ϊ7)=![]() =
=![]() .
.
(2)�٣��ٴ˴������С�5�㳯�ϡ���Ƶ��Ϊ20��60=![]() ��
��
��˵���Ǵ����.����������У���5�㳯�ϡ���Ƶ�������˵����5�㳯�ϡ���һ�¼������ĸ������.��Ϊ������Ĵ����ϴ�ʱ��Ƶ���ȶ��ڸ��ʣ���������ȫ���ڸ���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CΪ��ABD���Բ�ϵ�һ��������C����![]() �ϣ��Ҳ����B��D�غ�������ACB=��ABD=45����
�ϣ��Ҳ����B��D�غ�������ACB=��ABD=45����
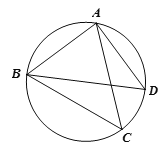
��1����֤��BD�Ǹ����Բ��ֱ����
��2������CD����֤��![]() AC=BC+CD��
AC=BC+CD��
��3������ABC����ֱ��AB�ĶԳ�ͼ��Ϊ��ABM������DM����̽��![]() ��
��![]() ����֮������ĵ�����ϵ����֤����Ľ��ۣ�
����֮������ĵ�����ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ��������з��̣�
��1����x+6��2��51
��2��x2��2x��2x��1
��3��x2��![]() x��2
x��2
��4��x��x��7����8��7��x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC��120����AB��AC��6��DΪ��AB��һ���㣨����B���غϣ�������CD�����߶�CD���ŵ�D��ʱ����ת90���õ�DE������BE����S��BDE�����ֵΪ_____��
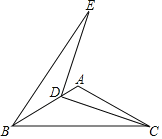
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ��һ��M��x,y����x��0������![]() ���kΪ��M������б��������ͼ����B��y�������ڵ�A����B������Ϊ(3,5),��PΪ��B�ϵĶ��㣬���P������б����k����Сֵ�ǣ� ��
���kΪ��M������б��������ͼ����B��y�������ڵ�A����B������Ϊ(3,5),��PΪ��B�ϵĶ��㣬���P������б����k����Сֵ�ǣ� ��
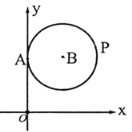
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ���������ĸ߶ȡ� �����ij��ѧ��ȤС���3��ͬѧѡ���˲���ѧУ����������ĸ߶ȣ���ͬһʱ�̵������������Ƿֱ��������¹�����
С�������һ����Ϊ1������͵�Ӱ��Ϊ0.8����������Ӱ��Ϊ4������ͼ1����
С��������������Ӱ�Ӳ�ȫ���ڵ���������һ����Ӱ�����ڽ�ѧ¥��ǽ��������ͼ2����ǽ���ϵ�Ӱ��Ϊ1.2�������ڵ����ϵ�Ӱ��Ϊ2.4����
С���������ı�����Ӱ�ӳ����ڵ�������������һ�������ڽ�ѧ¥�ĵ�һ��̨��������ͼ3������ô�Ӱ�ӳ�Ϊ0.3����һ��̨��Ϊ0.3�������ڵ����ϵ�Ӱ��Ϊ4.5����

��1���ں�����ֱ����д�����ĸ߶�Ϊ �ף�
��2����������ĸ߶ȣ�
��3����ѡ������ĸ߶�Ϊ�� ��
A��6.5�� B��5. 5�� C��6.3�� D��4.9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵ����ǰ���ͼ�ٰڷţ����С�A1CB1=��ACB=90�㣬��A1=��A=30�㣮
��1����ͼ���е���A1B1C˳ʱ����ת45����ͼ�ڣ���P1��A1C��AB�Ľ��㣬��Q��A1B1��BC�Ľ��㣬��֤��CP1=CQ��
��2����ͼ���У���AP1=2����CQ���ڶ��٣�
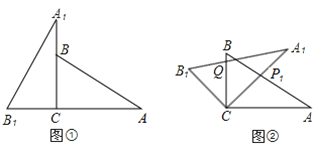
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲOΪԲ�ģ��뾶Ϊ1�Ļ�����������A��B���㣬P�ǻ�![]() ��һ�㣨����A��B�غϣ�������OP�����POB=�������P��������
��һ�㣨����A��B�غϣ�������OP�����POB=�������P��������

A. ��sin����sin���� B. ��cos����cos���� C. ��cos����sin���� D. ��sin����cos����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
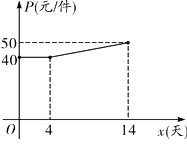
����Ŀ������ij��ҵ�ӵ�һ����Ʒ����������Ҫ�������14������ɣ���֪ÿ����Ʒ�ij�����Ϊ60Ԫ�����˼�x�������IJ�Ʒ����Ϊy����y��x�������¹�ϵ��
![]()
(1)���˼ڼ��������IJ�Ʒ����Ϊ70����
(2)���x�������IJ�Ʒ�ɱ�ΪPԪ/����P��![]() �ĺ���ͼ����ͼ�����˼�x�촴�������ΪWԪ����W��x�ĺ�����ϵʽ��������ڼ���ʱ���������������Ƕ��٣�
�ĺ���ͼ����ͼ�����˼�x�촴�������ΪWԪ����W��x�ĺ�����ϵʽ��������ڼ���ʱ���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com