【题目】用适当的方法解下列方程．
（1）（x+6）2＝51
（2）x2﹣2x＝2x﹣1
（3）x2﹣
x＝2
（4）x（x﹣7）＝8（7﹣x）
【答案】（1）x1＝﹣6+
, x2＝﹣6﹣；（2）x1＝2+
, x2＝2﹣；（3）x1＝
, x2＝
；（4）x1＝﹣8,x2＝7
【解析】
（1）根据直接开方法即可求出答案；
（2）根据配方法即可求出答案；
（3）根据公式法即可求出答案；
（4）根据因式分解法即可求出答案；
解：（1）∵（x+6）2＝51，
∴x+6＝±，
∴x1＝﹣6+, x2＝﹣6﹣；
（2）∵x2﹣2x＝2x﹣1，
∴x2﹣4x＝﹣1，
∴x2﹣4x+4＝3，
∴（x﹣2）2＝3，
∴x＝2±
∴x1＝2+, x2＝2﹣；
（3）原方程化为x2﹣
x﹣2＝0，
∴a＝1，b＝
，c＝﹣2，
∴△＝2+8＝10，
∴x＝
∴x1＝, x2＝；
（4）∵x（x﹣7）＝8（7﹣x），
∴x（x﹣7）﹣8（7﹣x）＝0，
∴（x+8）（x﹣7）＝0，
∴x1＝﹣8,x2＝7；
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角，墙DF足够长，墙DE长为9米，现用20米长的篱笆围成一个矩形花园ABCD，点C在墙DF上，点A在墙DE上，（篱笆只围AB，BC两边）．
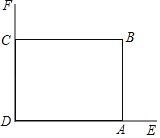
（Ⅰ）根据题意填表；
BC（m） | 1 | 3 | 5 | 7 |
矩形ABCD面积（m2） |
|
|
|
|
（Ⅱ）能够围成面积为100m2的矩形花园吗？如能说明围法，如不能，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
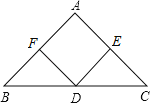
【题目】如图，在△ABC中，点D是边BC的中点，DE⊥AC、DF⊥AB，垂足分别是E、F，且BF=CE．
（1）求证：DE=DF；
（2）当∠A=90°时，试判断四边形AFDE是怎样的四边形，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
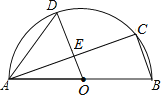
【题目】如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．
（1）若∠B=70°，求∠CAD的度数；
（2）若AB=4，AC=3，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝x2+bx+c的对称轴l交x轴于点A．
（1）若此抛物线经过点（1，2），当点A的坐标为（2，0）时，求此抛物线的解析式；
（2）抛物线y＝x2+bx+c交y轴于点B，将该抛物线平移，使其经过点A，B，且与x轴交于另一点C．若b2＝2c，b≤﹣1，比较线段OB与OC+
的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+
（a＞0，b＜0）的图象与x轴只有一个公共点A
（1）当a=时，求点A的坐标；
（2）过点A的直线y=x+k与二次函数的图象相交于另一点B，当b≥﹣1时，求点B的横坐标m的取值范围
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（4，3），B（9，3），将线段AB向下平移3个得到DC，其中点A与点D对应，点B与点C对应．
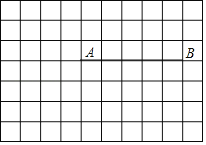
（1）画出线段DC，并直接写出点D的坐标 ；
（2）连接AD和BC得到四边形ABCD绕点D逆时针旋转90°后得到四边形EFGD，点A与E对应，点B与点F对应，点C与点G对应．
①请画出四边形EFGD，并直接写出点F的坐标 ；
②连接DB、DF、BF，△ABC的面积是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小颖和小红两名同学在学习“概率”时，做掷骰子（质地均匀的正方体）试验。
(1)小颖和小红在实验中如果各掷一枚骰子，那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明，并求出其最大概率。
(2)他们在一次实验中共掷骰子60次，试验的结果如下：
①填空：此次实验中“5点朝上”的频率为______；
②小红说：“根据实验，出现5点朝上的概率最大。”她的说法正确吗?为什么?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程x2－（m＋2）x＋（2m－1）=0。
（1）求证：方程恒有两个不相等的实数根；
（2）若此方程的一个根是1，请求出方程的另一个根，并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com