
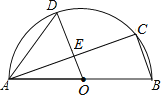
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
【答案】(1)35°;(2)2﹣![]() .
.
【解析】
试题(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得.
(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
试题解析:解:(1)∵AB是半圆O的直径,∴∠ACB=90°.
又∵OD∥BC,∴∠AEO=90°,即OE⊥AC.
∵∠B=70°,∴∠CAB=90°﹣∠B=90°﹣70°=20°.
∵OA=OD,∴∠DAO=∠ADO=55°.
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°.
(2)在Rt△ABC中,BC=![]() .
.
∵OE⊥AC,∴AE=EC.
又∵OA=OB,∴OE=![]() BC=
BC=![]() .
.
又∵OD=![]() AB=2,∴DE=OD﹣OE=2﹣
AB=2,∴DE=OD﹣OE=2﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)在下列表格中填上相应的值
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | -2 | 3 | 1 | … |

(2)若将上表中的变量![]() 用y来代替(即有
用y来代替(即有![]() ),请以表中的
),请以表中的![]() 的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
(3)在(2)的条件下,可将y看作是x的函数 ,请你结合你所画的图像,写出该函数图像的两个性质 :__________________________________________________.
(4)结合图像,借助之前所学的函数知识,直接写出不等式![]() 的解集: ____________
的解集: ____________
查看答案和解析>>
科目:初中数学 来源: 题型:
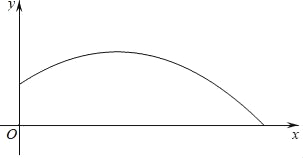
【题目】一名同学推铅球,铅球出手后行进过程中离地面的高度![]() (单位:
(单位:![]() )与水平距离
)与水平距离![]() (单位:
(单位:![]() )近似满足函数关系
)近似满足函数关系![]() ,其图象如图所示.已知铅球落地时的水平距离为
,其图象如图所示.已知铅球落地时的水平距离为![]() .
.
(1)求铅球出手时离地面的高度;
(2)在铅球行进过程中,当它离地面的高度为![]() 时,求此时铅球的水平距离.
时,求此时铅球的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
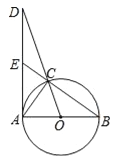
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形OABC的边OC、OA分别在x、y轴的正半轴上,设点B(4,4),点P(t,0)是x轴上一动点,过点O作OH⊥AP于点H,直线OH交直线BC于点D,连AD.
(1)如图1,当点P在线段OC上时,求证:OP=CD;
(2)在点P运动过程中,△AOP与以A、B、D为顶点的三角形相似时,求t的值;
(3)如图2,抛物线y=﹣![]() x2+
x2+![]() x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
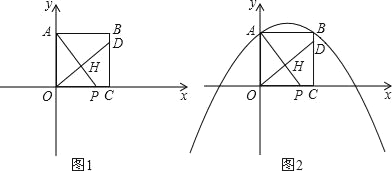
查看答案和解析>>
科目:初中数学 来源: 题型:
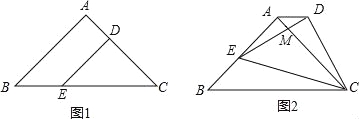
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2![]() ,D、E两点分别在AC、BC上,且DE∥AB,DC=2
,D、E两点分别在AC、BC上,且DE∥AB,DC=2![]() ,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
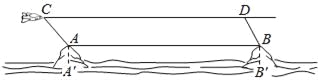
【题目】如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4![]() 米.
米.
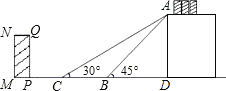
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com