
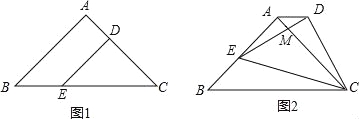
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2![]() ,D、E两点分别在AC、BC上,且DE∥AB,DC=2
,D、E两点分别在AC、BC上,且DE∥AB,DC=2![]() ,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
【答案】3![]() ﹣5.
﹣5.
【解析】
试题分析:如图1,∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵DE∥AB,
∴∠DEC=∠DCE=45°,∠EDC=90°,∴DE=CD=2![]() ,∴CE=CE′=4,
,∴CE=CE′=4,
如图2,在Rt△ACE′中,∠E′AC=90°,AC=2![]() ,CE′=4,
,CE′=4,
∴cos∠ACE′=![]() ,∴∠ACE′=30°,∴∠D′CA=∠E′CB=15°,
,∴∠ACE′=30°,∴∠D′CA=∠E′CB=15°,
又![]() =
=![]() =
=![]() ,∴△D′CA∽△E′CB,∴∠D′AC=∠B=45°,
,∴△D′CA∽△E′CB,∴∠D′AC=∠B=45°,
∴∠ACB=∠D′AC,∴AD′∥BC,
如图②过点C作CF⊥AD′,垂足为F,∵AD′∥BC,∴CF⊥BC.
∴∠FCD′=∠ACF﹣∠ACD′=30°.
在Rt△ACF中,AF=CF=![]() ,∴S△ACF=3,在Rt△D′CF中,CD′=2
,∴S△ACF=3,在Rt△D′CF中,CD′=2![]() ,∠FCD′=30°,
,∠FCD′=30°,
∴D′F=![]() ,∴S△D′CF=
,∴S△D′CF=![]() .
.
同理,SRt△AE′C=2![]() ,SRt△D′E′C=4,∵∠AME′=∠D′MC,∠E′AM=∠CD′M,
,SRt△D′E′C=4,∵∠AME′=∠D′MC,∠E′AM=∠CD′M,
∴△AME′∽△D′MC,∴![]() =
=![]() =
= =
=![]()
①∴S△AE′M=![]() S△CD′M.②∵S△EMC+S△AE′M=S△AE′C=2
S△CD′M.②∵S△EMC+S△AE′M=S△AE′C=2![]() ,
,
③S△E′MC+S△CD′M=S△D′EC=4.
由③﹣②,得S△C′DM﹣S△AE′M=4﹣2![]() ,
,
由①,得S△CD′M=8﹣4![]() ,
,
∴S△AD′M=S△ACF﹣S△DCF﹣S△CD′M=3![]() ﹣5.
﹣5.
∴△AD′M的面积是3![]() ﹣5.
﹣5.
故答案为:3![]() ﹣5.
﹣5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(10分)为支持亚太地区国家基础设施建设,由中国倡议设立亚投行,截止2015年4月15日,亚投行意向创始成员国确定为57个,其中意向创始成员国数亚洲是欧洲的2倍少2个,其余洲共5个,求亚洲和欧洲的意向创始成员国各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a.
如:1⊕3=1×32+2×1×3+1=16.
(1)求(﹣2)⊕3的值;
(2)若(a⊕3)⊕1=128,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
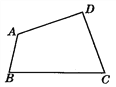
【题目】如图是一个大型模板,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com