
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4![]() 米.
米.
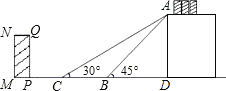
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据:![]() .
.
【答案】(1)AC的长度约为8米;(2)货物MNQP不应挪走.
【解析】
试题分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
解:(1)如图,
在Rt△ABD中,AD=ABsin45°=4![]() ×
×![]() =4.
=4.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走. (5分)
解:在Rt△ABD中,BD=ABcos45°=4![]() ×
×![]() =4.
=4.
在Rt△ACD中,CD=ACcos30°=2![]() .
.
∴CB=CD﹣BD=2![]() ﹣4≈0.9.
﹣4≈0.9.
∵PC=PB﹣CB≈4﹣0.9=3.1>2,
∴货物MNQP不应挪走.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
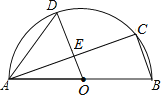
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示.
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -12 | -2 | 4 | 6 | 4 | … |
给出下列说法:①抛物线与y轴的交点为(0,6);②抛物线的对称轴是在y轴的右侧;③抛物线一定经过点(3,0);④当x<0时,函数值y随x的增大而减小.
从表中可知,上述说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
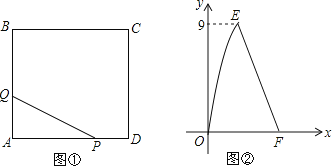
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点C(0,2),它的顶点为D(1,m),且
与y轴交于点C(0,2),它的顶点为D(1,m),且![]() .
.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,按照下列操作作图:①以A为圆心,AC长为半径画弧交AD的延长线于点E;②以E为圆心,EC长为半径画弧交DE的延长线于点F;③分别以C,F为圆心,大于![]() CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
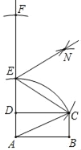
A. 54° B. 63° C. 72° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com