
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点C(0,2),它的顶点为D(1,m),且
与y轴交于点C(0,2),它的顶点为D(1,m),且![]() .
.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
【答案】(1)![]() (2)E(3,-1)(3)
(2)E(3,-1)(3)![]()
【解析】
(1)作DH⊥y轴,根据![]() ,求出m的值,再根据对称轴是x=1,和C,D两点求出抛物线的表达式即可;
,求出m的值,再根据对称轴是x=1,和C,D两点求出抛物线的表达式即可;
(2)设平移后的抛物线表达式为![]() ,然后得出OA=OB,得出B(0,2+k),A点的坐标为(2+k,0),然后代入求出k的值即可;
,然后得出OA=OB,得出B(0,2+k),A点的坐标为(2+k,0),然后代入求出k的值即可;
(3)设P(1,y),设对称轴与AB的交点为M,与x轴的交点为H,则H(1,0),由(2)得出A,B的坐标,然后得出![]() △BMP∽△BPA,然后根据
△BMP∽△BPA,然后根据![]()
解:(1)作DH⊥y轴,垂足为H,∵D(1,m)(![]() ),∴DH= m,HO=1.
),∴DH= m,HO=1.
∵![]() ,∴
,∴![]() ,∴m=3.
,∴m=3.
∴抛物线![]() 的顶点为D(1,3).
的顶点为D(1,3).
又∵抛物线![]() 与y轴交于点C(0,2),
与y轴交于点C(0,2),
∴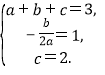 (2∴
(2∴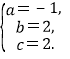 ∴抛物线的表达式为
∴抛物线的表达式为![]() .
.
(2)∵将此抛物线向上平移,
∴设平移后的抛物线表达式为![]() .
.
则它与y轴交点B(0,2+k).
∵平移后的抛物线与x轴正半轴交于点A,且OA=OB,∴A点的坐标为(2+k,0).
∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴A(3,0),抛物线![]() 向上平移了1个单位.
向上平移了1个单位.
∵点A由点E向上平移了1个单位所得,∴E(3,-1).
(3)由(2)得A(3,0),B(0, 3),∴![]() .
.
∵点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°,原顶点D(1,3),
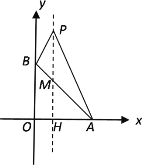
∴设P(1,y),设对称轴与AB的交点为M,与x轴的交点为H,则H(1,0).
∵A(3,0),B(0, 3),∴∠OAB=45°, ∴∠AMH=45°.
∴M(1,2). ∴![]() .
.
∵∠BMP=∠AMH, ∴∠BMP=45°.
∵∠APB=45°, ∴∠BMP=∠APB.
∵∠B=∠B,∴△BMP∽△BPA.
∴![]() .∴
.∴![]()
∴![]() .∴
.∴![]() (舍).
(舍).
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:正方形OABC的边OC、OA分别在x、y轴的正半轴上,设点B(4,4),点P(t,0)是x轴上一动点,过点O作OH⊥AP于点H,直线OH交直线BC于点D,连AD.
(1)如图1,当点P在线段OC上时,求证:OP=CD;
(2)在点P运动过程中,△AOP与以A、B、D为顶点的三角形相似时,求t的值;
(3)如图2,抛物线y=﹣![]() x2+
x2+![]() x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
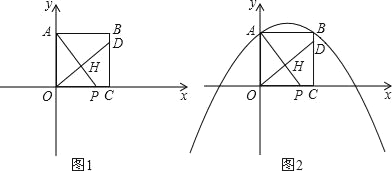
查看答案和解析>>
科目:初中数学 来源: 题型:
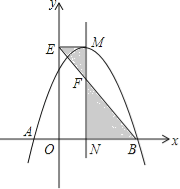
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租用4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4![]() 米.
米.
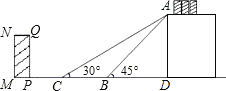
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
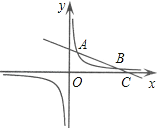
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
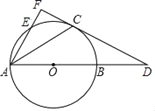
【题目】如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.
(1)求证:DC是⊙O的切线;
(2)若⊙O的半径为3,sin∠D=![]() ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图并填空
如图,在Rt△ABC,∠BAC=90°,AD⊥BC于D,在②③图中,MN=AB,∠MNE=∠B,现要以②③图为基础,在射线NE上确定一点P,构造出一个△MNP与①图中某一个三角形全等.
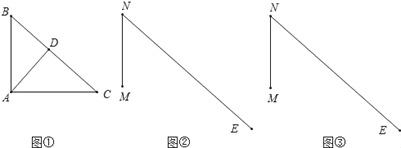
(1)用边长限制P点,画法:_____,可根据SAS,AAS,ASA,HL中的______得到______.
(2)用直角限制点P,画法:_______,可根据SAS,AAS,ASA,HL中的______得到______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx﹣1交y轴于点B,交x轴于点C,以BC为边的正方形ABCD的顶点A(﹣1,a)在双曲线y=﹣![]() (x<0)上,D点在双曲线y=
(x<0)上,D点在双曲线y=![]() (x>0)上,则k的值为( )
(x>0)上,则k的值为( )
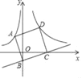
A. 6 B. 5 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com