
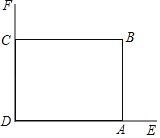
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为9米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
(Ⅰ)根据题意填表;
BC(m) | 1 | 3 | 5 | 7 |
矩形ABCD面积(m2) |
|
|
|
|
(Ⅱ)能够围成面积为100m2的矩形花园吗?如能说明围法,如不能,说明理由.
【答案】(Ⅰ)19;51;75;91(II)不能,理由见解析
【解析】
(I)利用矩形的面积=长×宽,即可求出结论;
(II)设BC=xm,则AB=(20﹣x)m,利用矩形的面积公式结合矩形的花园的面积为100m2,即可得出关于x的一元二次方程,解之即可求出x的值,由x不超过9可得出不能围成面积为100m2的矩形花园.
解:(I)1×(20﹣1)=19,3×(20﹣3)=51,5×(20﹣5)=75,7×(20﹣7)=91.
故答案为:19;51;75;91.
(II)不能,理由如下;
设BC=xm,则AB=(20﹣x)m,
依题意,得:x(20﹣x)=100,
整理,得:x2﹣20x+100=0,
解得:x1=x2=10.
∵10>9,
∴不能围成面积为100m2的矩形花园.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.三角形ABC的三个顶点均在格点上,以点A为圆心的弧EF与BC相切于格点D,分别交AB,AC于点E,F.
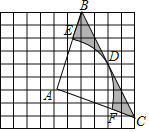
(1)直接写出三角形ABC边长AB= ;AC= ;BC= .
(2)求图中由线段EB,BC,CF及弧FE所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
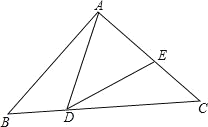
【题目】如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值?
(3)在AC上是否存在点E,使△ADE是等腰三角形?若存在,求AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.直角尺的直角顶点放在点P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).
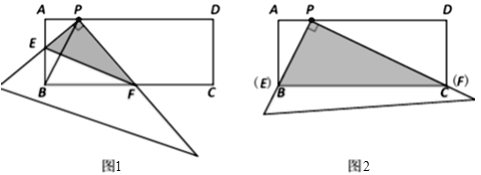
(1)当点E与点B重合时,点F恰好与点C重合(如图2).
①求证:△APB∽△DCP;
②求PC、BC的长.
(2)探究:将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中(图1是该过程的某个时刻),观察、猜想并解答:
① tan∠PEF的值是否发生变化?请说明理由.
② 设AE=x,当△PBF是等腰三角形时,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验:
(1)已知抛物线y=﹣x2+bx﹣3经过点(﹣1,0),则b= ,顶点坐标 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式是 .
抽象感悟:
我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M对称的抛物线y',则我们又称抛物线y'为抛物线y的“衍生抛物线”,点M为“衍生中心”.
(2)已知抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y',若这两条抛物线有交点,求m的取值范围.
问题解决:
(3)已知抛物线y=ax2+2ax﹣b(a≠0)若抛物线y的衍生抛物线为y'=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a,b的值及衍生中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
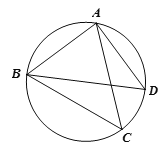
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com