
【题目】小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验:
(1)已知抛物线y=﹣x2+bx﹣3经过点(﹣1,0),则b= ,顶点坐标 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式是 .
抽象感悟:
我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M对称的抛物线y',则我们又称抛物线y'为抛物线y的“衍生抛物线”,点M为“衍生中心”.
(2)已知抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y',若这两条抛物线有交点,求m的取值范围.
问题解决:
(3)已知抛物线y=ax2+2ax﹣b(a≠0)若抛物线y的衍生抛物线为y'=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a,b的值及衍生中心的坐标.
【答案】(1)﹣4,(﹣2,1),y=x2﹣4x+5; (2)m≤5;(3)a=3,b=﹣3,衍生中心的坐标为(0,6);
【解析】
求解体验:(1)利用待定系数法求出b的值,进而求出顶点坐标,在抛物线上取一点(0,﹣3),求出点(﹣2,1)和(0,﹣3)关于(0,1)的对称点坐标,利用待定系数法即可得出结论;
抽象感悟:(2)求出抛物线的顶点坐标(﹣1,6),进而利用待定系数法求出衍生函数解析式,联立即可得出结论;
问题解决:(3)①求出抛物线的顶点坐标和衍生抛物线的顶点坐标,分别代入抛物线解析式中,即可求出a,b的值,即可得出结论;
解:求解体验:
(1)∵抛物线y=﹣x2+bx﹣3经过点(﹣1,0),
∴﹣1﹣b﹣3=0,
∴b=﹣4,
∴抛物线解析式为y=﹣x2﹣4x﹣3=﹣(x+2)2+1,
∴抛物线的顶点坐标为(﹣2,1),
∴抛物线的顶点坐标(﹣2,1)关于(0,1)的对称点为(2,1),
即:新抛物线的顶点坐标为(2,1),
令原抛物线的x=0,
∴y=﹣3,
∴(0,﹣3)关于点(0,1)的对称点坐标为(0,5),
设新抛物线的解析式为y=a(x﹣2)2+1,
∵点(0,5)在新抛物线上,
∴5=a(0﹣2)2+1,
∴a=1,
∴新抛物线解析式为y=(x﹣2)2+1=x2﹣4x+5,
故答案为:﹣4,(﹣2,1),y=x2﹣4x+5;
抽象感悟:
(2)∵抛物线y=﹣x2﹣2x+5=﹣(x+1)2+6①,
∴抛物线的顶点坐标为(﹣1,6),
设衍生抛物线为y′=a(x﹣1)2+2m﹣6,
∵抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y′,
∴a=1,
∴衍生抛物线为y′=(x﹣1)2+2m﹣6=x2﹣2x+2m﹣5②,
联立①②得,x2﹣2x+2m﹣5=﹣x2﹣2x+5,
整理得,2x2=10﹣2m,
∵这两条抛物线有交点,
∴10﹣2m≥0,
∴m≤5;
问题解决:
(3)①抛物线y=ax2+2ax﹣b=a(x+1)2﹣a﹣b,
∴此抛物线的顶点坐标为(﹣1,﹣a﹣b),
∵抛物线y的衍生抛物线为y′=bx2﹣2bx+a2=b(x﹣1)2+a2﹣b,
∴a+b=0,③
∵两个抛物线有两个交点,且恰好是它们的顶点,
∴b+2b+a2=﹣a﹣b④,
联立③④,得:
a=0(舍)或a=3,
∴b=﹣3,
∴抛物线y的顶点坐标为(﹣1,0),抛物线y的衍生抛物线的顶点坐标为(1,12),
∴衍生中心的坐标为:(0,6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
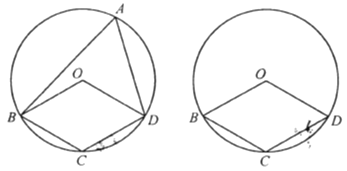
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,
内部,![]() 时,
时,![]() ________.
________.
(2)当圆心![]() 在
在![]() 内部,四边形
内部,四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的度数;
的度数;
(3)当圆心![]() 在
在![]() 外部,四边形
外部,四边形![]() 为平行四边形时,请直接写出
为平行四边形时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.


作法:如图,
①作射线OP;
②在直线OP外任取一点A,以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.
根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴∠BPC=90°(____________)(填推理的依据).
∴OP⊥PC.
又∵OP是⊙O的半径,
∴PC是⊙O的切线(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为9米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
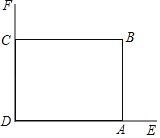
(Ⅰ)根据题意填表;
BC(m) | 1 | 3 | 5 | 7 |
矩形ABCD面积(m2) |
|
|
|
|
(Ⅱ)能够围成面积为100m2的矩形花园吗?如能说明围法,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
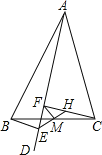
A.M是BC的中点B.FM=![]() EH
EH
C.CF⊥ADD.FM⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数关系式中,二次函数的个数有( )
(1)y=3(x-1)2+1 (2)y=![]() (3)S=3-2t2 (4)y= x4+2x2-1 (5)y=3x(2-x)+ 3x2 (6) y=mx2+x
(3)S=3-2t2 (4)y= x4+2x2-1 (5)y=3x(2-x)+ 3x2 (6) y=mx2+x
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=-x2+bx+c经过A(-3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.
(1)求抛物线C的表达式;
(2)求点M的坐标;
(3)将抛物线C平移到抛物线C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
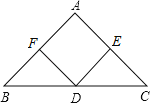
【题目】如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.
(1)求证:DE=DF;
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(4,3),B(9,3),将线段AB向下平移3个得到DC,其中点A与点D对应,点B与点C对应.
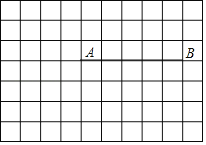
(1)画出线段DC,并直接写出点D的坐标 ;
(2)连接AD和BC得到四边形ABCD绕点D逆时针旋转90°后得到四边形EFGD,点A与E对应,点B与点F对应,点C与点G对应.
①请画出四边形EFGD,并直接写出点F的坐标 ;
②连接DB、DF、BF,△ABC的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com