
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,
内部,![]() 时,
时,![]() ________.
________.
(2)当圆心![]() 在
在![]() 内部,四边形
内部,四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的度数;
的度数;
(3)当圆心![]() 在
在![]() 外部,四边形
外部,四边形![]() 为平行四边形时,请直接写出
为平行四边形时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
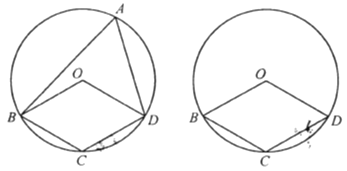
【答案】120
【解析】试题分析:(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠OAB+∠OAD=∠ABO+∠ADO=60°,然后根据圆周角定理易得∠BOD=2∠BAD=120°;
(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠A,则∠BCD=2∠A,然后根据圆内接四边形的性质由∠BCD+∠A=180°,易计算出∠A的度数;
(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD-∠OAB=∠ADO-∠ABO=∠BAD,由(2)得∠BAD=60°,
所以∠ADO-∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO-∠ADO=60°.
解: (1)连接OA,如图1,
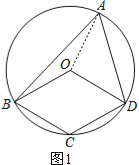
∵OA=OB,OA=OD,
∵∠OAB=∠ABO,∠OAD=∠ADO,
∴∠OAB+∠OAD=∠ABO+∠ADO=60°,即∠BAD=60°,
∴∠BOD=2∠BAD=120°;
故答案为120°;
(2)∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,
∵∠BOD=2∠A,
∴∠BCD=2∠A,
∵∠BCD+∠A=180°,即3∠A=180°,
∴∠A=60°;
(3)当∠OAB比∠ODA小时,如图2,
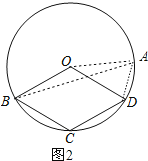
∵OA=OB,OA=OD,
∵∠OAB=∠ABO,∠OAD=∠ADO,
∴∠OAD∠OAB=∠ADO∠ABO=∠BAD,
由(2)得∠BAD=60°,
∴∠ADO∠ABO=60°;
当∠OAB比∠ODA大时,
同理可得∠ABO∠ADO=60°,
综上所述,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
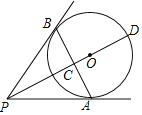
A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备进一批每个进价为40元的小家电,经市场调查预测,售价定为50元时可售出400个;定价每增加1元,销售量将减少10个.
(1)设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)
(2)超市若准备获得利润6000元,并且使进货量较少,则每个应定价为多少元?
(3)超市若要获得最大利润,则每个应定价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
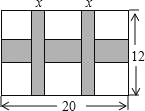
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为![]() m,DC的长为
m,DC的长为![]() m。
m。
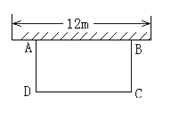
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量![]() 能否取值为4m,若能,求出
能否取值为4m,若能,求出![]() 的值,若不能,请说明理由;
的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验:
(1)已知抛物线y=﹣x2+bx﹣3经过点(﹣1,0),则b= ,顶点坐标 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式是 .
抽象感悟:
我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M对称的抛物线y',则我们又称抛物线y'为抛物线y的“衍生抛物线”,点M为“衍生中心”.
(2)已知抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y',若这两条抛物线有交点,求m的取值范围.
问题解决:
(3)已知抛物线y=ax2+2ax﹣b(a≠0)若抛物线y的衍生抛物线为y'=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a,b的值及衍生中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com