
ЁОЬтФПЁПдкОиаЮABCDжаЃЌЕуPдкADЩЯЃЌAB=2ЃЌAP=1.жБНЧГпЕФжБНЧЖЅЕуЗХдкЕуPДІЃЌжБНЧГпЕФСНБпЗжБ№НЛABЁЂBCгкЕуEЁЂFЃЌСЌНгEF(ШчЭМ1).
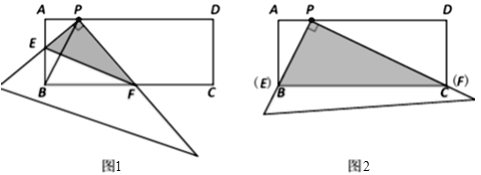
(1)ЕБЕуEгыЕуBжиКЯЪБЃЌЕуFЧЁКУгыЕуCжиКЯ(ШчЭМ2).
ЂйЧѓжЄЃКЁїAPBЁзЁїDCPЃЛ
ЂкЧѓPCЁЂBCЕФГЄ.
(2)ЬНОПЃКНЋжБНЧГпДгЭМ2жаЕФЮЛжУПЊЪМЃЌШЦЕуPЫГЪБеыа§зЊЃЌЕБЕуEКЭЕуAжиКЯЪБЭЃжЙ.дкетИіЙ§ГЬжа(ЭМ1ЪЧИУЙ§ГЬЕФФГИіЪБПЬ)ЃЌЙлВьЁЂВТЯыВЂНтД№ЃК
Ђй tanЁЯPEFЕФжЕЪЧЗёЗЂЩњБфЛЏЃПЧыЫЕУїРэгЩ.
Ђк ЩшAE=xЃЌЕБЁїPBFЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіxЕФжЕ.
ЁОД№АИЁП(1)ЂйжЄУїМћНтЮіЃЛЂкPC=2![]() ЃЌBC=5ЃЛ(2)ЂйtanЁЯPEFЕФжЕВЛБфЃЛЂкx=
ЃЌBC=5ЃЛ(2)ЂйtanЁЯPEFЕФжЕВЛБфЃЛЂкx=![]() Лђx=
Лђx=![]() Лђx=
Лђx=![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйгЩЙДЙЩЖЈРэЧѓBPЃЌРћгУЛЅгрЙиЯЕжЄУїЁїAPBЁзЁїDCPЃЛЂкРћгУЯрЫЦБШЧѓPCЃЌDP, дйИљОнBC=AD=AP+DPМДПЩЧѓЕУBCЕФГЄЃЛ
ЃЈ2ЃЉЂйtanЁЯPEFЕФжЕВЛБфЃЎРэгЩЮЊЃКЙ§FзїFGЁЭADЃЌДЙзуЮЊЕуG. дђЫФБпаЮABFGЪЧОиаЮЃЌЭЌЃЈ1ЃЉЕФЗНЗЈжЄУїЁїAPEЁзЁїGFPЃЌЕУЯрЫЦБШ![]() ЃЌдйРћгУШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓжЕЃЛЂкРћгУЯрЫЦБШЧѓGPЃЌдйОиаЮаджЪЧѓГіBFЃЌЁїPBFЪЧЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіЬжТлЃК(Ђё) ЕБPB=PFЪБЃЌИљОнBF=2APЧѓжЕЃЛЕБBF=BPЪБЃЌ(Ђђ)ИљОнBP=
ЃЌдйРћгУШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓжЕЃЛЂкРћгУЯрЫЦБШЧѓGPЃЌдйОиаЮаджЪЧѓГіBFЃЌЁїPBFЪЧЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіЬжТлЃК(Ђё) ЕБPB=PFЪБЃЌИљОнBF=2APЧѓжЕЃЛЕБBF=BPЪБЃЌ(Ђђ)ИљОнBP=![]() ЧѓжЕЃЛ(Ђѓ) ЕБBF=PFЪБЃЌИљОнPF=
ЧѓжЕЃЛ(Ђѓ) ЕБBF=PFЪБЃЌИљОнPF=![]() МДПЩЧѓГіxжЕ.
МДПЩЧѓГіxжЕ.
НтЃК(1)ЂйШчЭМ3.2ЃЌ
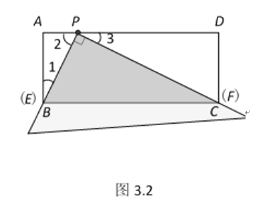
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯA=ЁЯD=90ЁуЃЌCD=AB=2ЃЌ
ЁрдкRtЁїABCжаЃЌ
ЁЯ1+ЁЯ2=90ЁуЃЌBP=![]() .
.
гжЁпЁЯBPC=90Ёу,
ЁрЁЯ3+ЁЯ2=90ЁуЃЌ
ЁрЁЯ1=ЁЯ3.
ЁрЁїAPBЁзЁїDCP.
ЂкгЩЁїAPBЁзЁїDCP.
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
ЁрPC=2![]() ЃЌDP=4.
ЃЌDP=4.
ЁрBC=AD=AP+DP=5.
(2)ЂйtanЁЯPEFЕФжЕВЛБф.
РэгЩШчЯТЃК
ШчЭМ3.1ЃЌЙ§FзїFGЁЭADЃЌДЙзуЮЊЕуG. дђЫФБпаЮABFGЪЧОиаЮ.
ЁрЁЯA=ЁЯPGF=90ЁуЃЌFG=AB=2ЃЌ
ЁрдкRtЁїAPEжаЃЌЁЯ1+ЁЯ2=90ЁуЃЌ
гжЁпЁЯEPF=90Ёу,ЁрЁЯ3+ЁЯ2=90ЁуЃЌ
ЁрЁЯ1=ЁЯ3.
ЁрЁїAPEЁзЁїGFPЃЌ
Ёр![]() .
.
ЁрдкRtЁїEPFжаЃЌtanЁЯPEF=![]() 2.
2.
ЁрtanЁЯPEFЕФжЕВЛБф.
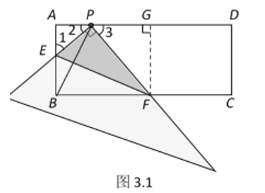
ЂкгЩЁїAPEЁзЁїGFP.
Ёр![]() .
.
ЁрGP=2AE=2xЃЌ
ЁпЫФБпаЮABFGЪЧОиаЮ.
ЁрBF=AG=AP+GP=2x+1.
ЁїPBFЪЧЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіЬжТлЃК
(Ђё)ЕБPB=PFЪБЃЌЕуPдкBFЕФДЙжБЦНЗжЯпЩЯ.
Ёр BF=2AP. МД2x+1=2ЃЌ
Ёрx=![]() .
.
(Ђђ)ЕБBF=BPЪБЃЌ
BP=![]() BP=
BP=![]()
Ёр2x+1=![]() .
.
Ёрx=![]() .
.
(Ђѓ)ЕБBF=PFЪБЃЌ
ЁпPF=![]() ЃЌ
ЃЌ
Ёр(2x)2+22=(2x+1)2ЃЌ
Ёрx=![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЪЧвдЕу
ЪЧвдЕу![]() ЃЈ0,3ЃЉЮЊдВаФЃЌ2ЮЊАыОЖЕФдВЩЯЕФЖЏЕуЃЌ
ЃЈ0,3ЃЉЮЊдВаФЃЌ2ЮЊАыОЖЕФдВЩЯЕФЖЏЕуЃЌ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌСЌНс
ЕФжаЕуЃЌСЌНс![]() .дђЯпЖЮ
.дђЯпЖЮ![]() ЕФзюДѓжЕЪЧЃЈ ЃЉ
ЕФзюДѓжЕЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
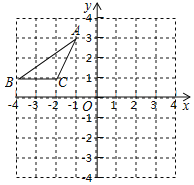
ЁОЬтФПЁПЃЈ2016КкСњНЪЁСњЖЋЕиЧјЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ3ЃЉЁЂЃЈЉ4ЃЌ1ЃЉЃЈЉ2ЃЌ1ЃЉЃЌЯШНЋЁїABCбивЛШЗЖЈЗНЯђЦНвЦЕУЕНЁїA1B1C1ЃЌЕуBЕФЖдгІЕуB1ЕФзјБъЪЧЃЈ1ЃЌ2ЃЉЃЌдйНЋЁїA1B1C1ШЦдЕуOЫГЪБеыа§зЊ90ЁуЕУЕНЁїA2B2C2ЃЌЕуA1ЕФЖдгІЕуЮЊЕуA2ЃЎ
ЃЈ1ЃЉЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉЧѓГідкетСНДЮБфЛЛЙ§ГЬжаЃЌЕуAОЙ§ЕуA1ЕНДяA2ЕФТЗОЖзмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
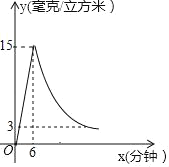
ЁОЬтФПЁПЮЊСЫдЄЗРЁАСїИаЁАЃЌФГбЇаЃЖдНЬЪвВЩгУбЌЗЈНјааЯћЖОЃЌвбжЊвЉЮяШМЩеЪБЃЎЪвФкУПСЂЗНУзПеЦјжаЕФКЌвЉСПyЃЈКСПЫ/СЂЗНУзЃЉгывЉЮяЕуШМКѓЕФЪБМфxЃЈЗжжгЃЉГЩе§БШР§ЃЛвЉЮяШМОЁКѓЃЌyгыxГЩЗДБШР§ЃЈШчЭМЫљЪОЃЉвбжЊвЉЮяЕуШМКѓ6ЗжжгШМОЁЃЌДЫЪБЪвФкУПСЂЗНУзПеЦјжаКЌвЉСПЮЊ15КСПЫЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГіетСНИіКЏЪ§ЕФБэДяЪНЃК
ЃЈ2ЃЉбаОПБэУїЃЌЕБПеЦјжаУПСЂЗНУзЕФКЌвЉСПЕЭгк3КСПЫЪБЖдШЫЬхУЛгаЮЃКІЃЌФЧУДДЫДЮЯћЖОКѓОЙ§ЖрГЄЪБМфбЇЩњВХПЩвдАВШЋНјШыНЬЪвЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкУРЛЏаЃдАЕФЛюЖЏжаЃЌФГаЫШЄаЁзщЯыНшжњШчЭМЫљЪОЕФжБНЧЧННЧЃЌЧНDFзуЙЛГЄЃЌЧНDEГЄЮЊ9УзЃЌЯжгУ20УзГЄЕФРщАЪЮЇГЩвЛИіОиаЮЛЈдАABCDЃЌЕуCдкЧНDFЩЯЃЌЕуAдкЧНDEЩЯЃЌЃЈРщАЪжЛЮЇABЃЌBCСНБпЃЉЃЎ
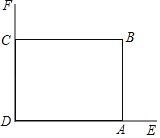
ЃЈЂёЃЉИљОнЬтвтЬюБэЃЛ
BCЃЈmЃЉ | 1 | 3 | 5 | 7 |
ОиаЮABCDУцЛ§ЃЈm2ЃЉ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЃЈЂђЃЉФмЙЛЮЇГЩУцЛ§ЮЊ100m2ЕФОиаЮЛЈдАТ№ЃПШчФмЫЕУїЮЇЗЈЃЌШчВЛФмЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
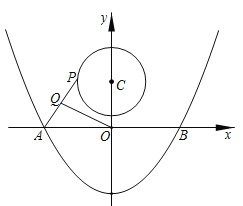
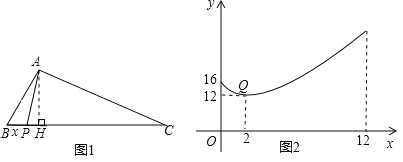
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЕуPЮЊBCБпЩЯвЛЕуЃЌЩшBPЃНxЃЌAP2ЃНyЃЌвбжЊyЪЧxЕФЖўДЮКЏЪ§ЕФвЛВПЗжЃЌЦфЭМЯѓШчЭМ2ЃЌЕуQЃЈ2ЃЌ12ЃЉЪЧЭМЯѓЩЯЕФзюЕЭЕуЃЌЧвЭМЯѓгыyжсНЛгкЃЈ0ЃЌ16ЃЉЃЎ
ЃЈ1ЃЉЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕБЁїABPЮЊжБНЧШ§НЧаЮЪБЃЌBPЕФжЕЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаКЏЪ§ЙиЯЕЪНжаЃЌЖўДЮКЏЪ§ЕФИіЪ§гаЃЈ ЃЉ
ЃЈ1ЃЉy=3(xЃ1)2+1 ЃЈ2ЃЉy=![]() ЃЈ3ЃЉS=3Ѓ2t2 ЃЈ4ЃЉyЃН x4ЃЋ2x2Ѓ1 ЃЈ5ЃЉyЃН3x(2Ѓx)ЃЋ 3x2 (6) y=mx2+x
ЃЈ3ЃЉS=3Ѓ2t2 ЃЈ4ЃЉyЃН x4ЃЋ2x2Ѓ1 ЃЈ5ЃЉyЃН3x(2Ѓx)ЃЋ 3x2 (6) y=mx2+x
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁСѕЭЌбЇдкПЮЭтЛюЖЏжаЙлВьЕѕГЕЕФЙЄзїЙ§ГЬЃЌЛцжЦСЫШчЭМЫљЪОЕФЦНУцЭМаЮЃЎвбжЊЕѕГЕЕѕБлЕФжЇЕуOОрРыЕиУцЕФИпOOЁф=2УзЃЎЕБЕѕБлЖЅЖЫгЩAЕуЬЇЩ§жСAЁфЕуЃЈЕѕБлГЄЖШВЛБфЃЉЪБЃЌЕиУцBДІЕФжиЮяЃЈДѓаЁКіТдВЛМЦЃЉБЛЕѕжСBЁфДІЃЌНєБСзХЕФЕѕРТAЁфBЁф=ABЃЎABДЙжБЕиУцOЁфBгкЕуBЃЌAЁфBЁфДЙжБЕиУцOЁфBгкЕуCЃЌЕѕБлГЄЖШOAЁф=OA=10УзЃЌЧвcosA=![]() ЃЌsinAЁф=
ЃЌsinAЁф=![]() ЃЎ
ЃЎ
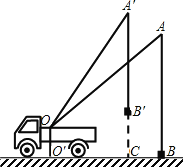
ЃЈ1ЃЉЧѓДЫжиЮядкЫЎЦНЗНЯђвЦЖЏЕФОрРыBCЃЛ
ЃЈ2ЃЉЧѓДЫжиЮядкЪњжБЗНЯђвЦЖЏЕФОрРыBЁфCЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+![]() ЃЈaЃО0ЃЌbЃМ0ЃЉЕФЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуA
ЃЈaЃО0ЃЌbЃМ0ЃЉЕФЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуA
ЃЈ1ЃЉЕБa=![]() ЪБЃЌЧѓЕуAЕФзјБъЃЛ
ЪБЃЌЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЙ§ЕуAЕФжБЯпy=x+kгыЖўДЮКЏЪ§ЕФЭМЯѓЯрНЛгкСэвЛЕуBЃЌЕБbЁнЉ1ЪБЃЌЧѓЕуBЕФКсзјБъmЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com