
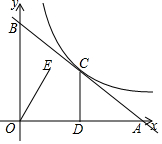
 ��ͼ��һ�κ���y=-$\frac{3}{4}$x+3��ͼ����x�ᣬy��ֱ���A��B���㣬�뷴��������y=$\frac{k}{x}$��x��0����ͼ���ڵ�C��2��n��������C��CD��x�ᣬ����ΪD��
��ͼ��һ�κ���y=-$\frac{3}{4}$x+3��ͼ����x�ᣬy��ֱ���A��B���㣬�뷴��������y=$\frac{k}{x}$��x��0����ͼ���ڵ�C��2��n��������C��CD��x�ᣬ����ΪD������ ��1����ȷ������C�����꣬���뷴������������ʽ�м��ɵó�k��
��2������ȷ����ֱ��OE�Ľ���ʽ�������M���꣬���뷴������������ʽ�У�ֱ�����n��ƽ�����������m��ֵ��
��3�����жϳ�EA+$\frac{2}{3}$EB��Сʱ���������жϳ�����A��ֱ�ߺ���OΪԲ�ģ�2Ϊ�뾶��Բ�����ȡ����С��
��� �⣺��1���ߵ�C��2��n����ֱ��y=-$\frac{3}{4}$x+3�ϣ�
��n=-$\frac{3}{4}$��2+3=$\frac{3}{2}$��
��C��2��$\frac{3}{2}$����
�ߵ�C�ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�
��k=2��$\frac{3}{2}$=3��
��2������ͼ1��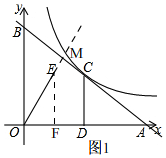 ����E��EF��OA��
����E��EF��OA��
����ת֪��OE=OD=2����EOF=60�㣬
��OF=1��EF=$\sqrt{3}$��
��E��1��$\sqrt{3}$����
��ֱ��OE�Ľ���ʽΪy=$\sqrt{3}$x��
���M��n��$\sqrt{3}$n����
�ɣ�1��֪��k=3��
�෴������������ʽΪy=$\frac{3}{x}$��
�ߵ�M�ڷ����������ϣ�
��$\sqrt{3}$n=$\frac{3}{n}$��
��n2=$\frac{\sqrt{3}}{3}$��
��m2=OM2=n2+��$\sqrt{3}$n��2=4n2=4��$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$��
����ͼ2��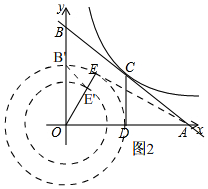
���E��p��q����
��B��0��3����
��$\frac{2}{3}$EB=$\frac{2}{3}$$\sqrt{{p}^{2}+��q-3��^{2}}$=$\sqrt{��\frac{2}{3}p��^{2}+��\frac{2}{3}q-2��^{2}}$��
��$\frac{2}{3}$p��$\frac{2}{3}$q��������E'����ʾ�߶�OE����ԭ��ľ�����$\frac{2}{3}$OE��
��0��2������B'��
��$\sqrt{��\frac{2}{3}p��^{2}+��\frac{2}{3}q-2��^{2}}$��ʾ���ǵ�B'����E'�ľ��룬
��B'E'��OE��AE��OEʱ��EA+$\frac{2}{3}$EB��С��
��Rt��AOE��OA=4��OC=2��
��cos��=cos��AOE=$\frac{OE}{OA}$=$\frac{1}{2}$��
���� �����Ƿ����������ۺ��⣬��Ҫ�����˴���ϵ������ƽ������ϵ�ڣ������ľ��빫ʽ��ȷ����k�ǽⱾ��Ĺؼ����жϳ�EA+$\frac{2}{3}$EB��Сʱ�������ǽⱾ����ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ۺ���̽��
�ۺ���̽���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
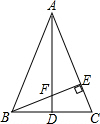 ��ͼ����ABC�У�AB=AC��BE��AC�ڵ�E��AD��BC�ڵ�D����ABE=45�㣬AD��BE���ڵ�F������CF��
��ͼ����ABC�У�AB=AC��BE��AC�ڵ�E��AD��BC�ڵ�D����ABE=45�㣬AD��BE���ڵ�F������CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
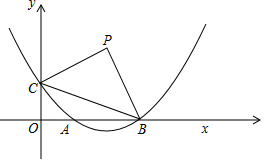 ��֪����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2-4ax+1��x��������ύ�ڵ�A�͵�B����y�ύ�ڵ�C����OB=3OC����P�ǵ�һ�����ڵĵ㣬����BC����PBC����BCΪб�ߵĵ���ֱ�������Σ�
��֪����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2-4ax+1��x��������ύ�ڵ�A�͵�B����y�ύ�ڵ�C����OB=3OC����P�ǵ�һ�����ڵĵ㣬����BC����PBC����BCΪб�ߵĵ���ֱ�������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com