
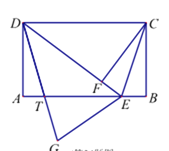
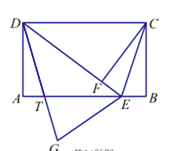
【题目】如图,在四边形ABCD中,AB∥CD,点E在AB上,AB=DC=DE, AD⊥AB,BC⊥AB,CF⊥DE,垂足分别为点A,B,F,AD=BC=6,EB=2.
(1)求证:CF=CB;
(2)求△DEC的面积S的值;
(3)若将△DEC沿着DE翻折得到△DEG,DG交AB于点T,试判断线段DT与CE的长度是否相等:并说明理由.
【答案】(1)证明见解析;(2)30;(3)不相等,理由见解析.
【解析】
(1)根据AB∥CD,可得∠CDE=∠DEA,由AD⊥AB,CF⊥DE,可得∠A=∠CFD=90°,然后根据AAS定理证明△DCF≌△EDA,从而得到CF=DA,问题得解;(2)利用CF=CB,CE=CE,根据HL定理证明Rt△CFE≌Rt△CBE,得到EF=EB=2,设DE=DC=x,利用勾股定理列方程求DE的长,从而求出三角形面积;(3)利用勾股定理求出CE的长,然后根据折叠的性质和平行线的性质,可得DT=TE,设DT=TE=y,在Rt△DAT中,列方程求DT的长,从而求证问题.
解:(1)∵AB∥CD
∴∠CDE=∠DEA
∵AD⊥AB,CF⊥DE
∴∠A=∠CFD=90°
又∵DC=DE
∴△DCF≌△EDA
∴CF=DA
∵AD=BC
∴CF=CB
(2)∵BC⊥AB,CF⊥DE
∴∠B=∠CFE=90°
又∵CF=CB,CE=CE
∴Rt△CFE≌Rt△CBE(HL)
∴∠CFD=∠B=90°,CF=BC=6,EF=EB=2
设DE=DC=x,则DF=x-2
由题意,在Rt△DFC中,![]()
解得:x=10
∴![]()
(3)由题意可知,在Rt△BCE中,![]()
由折叠性质可知,∠TDE=∠CDE
∵AB∥CD
∴∠CDE=∠DEA
∴∠TDE=∠DEA
∴DT=TE
设DT=TE=y,则AT=10-2-y=8-y
在Rt△DAT中,![]()
解得:![]()
∴DT与CE的长度不相等


科目:初中数学 来源: 题型:
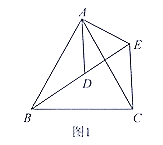
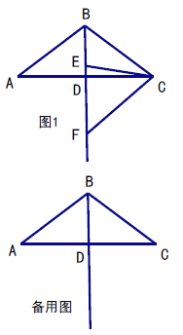
【题目】(1)问题发现:如图1, ![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接
在同一直线上,连接![]()
①求证:![]() ; ②求
; ②求![]() 的度数.
的度数.
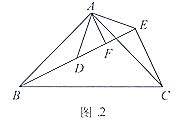
(2)拓展探究:如图2, ![]()
![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上
在同一直线上![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]()
①求![]() 的度数:
的度数:
②判断线段![]() 之间的数量关系(直接写出结果即可).
之间的数量关系(直接写出结果即可).
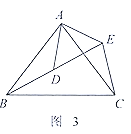
![]() 解决问题:如图3,
解决问题:如图3,![]() 和
和![]() 均为等腰三角形,
均为等腰三角形,![]() ,点
,点![]() 在同一直线上,连接
在同一直线上,连接![]() .求
.求![]() 的度数(用含
的度数(用含![]() 的代数式表示,直接写出结果即可).
的代数式表示,直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.
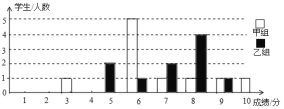
(1)补充完成下面的成绩统计分析表:
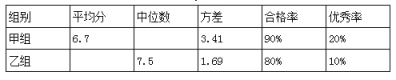
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,求x的取值范围;
时,求x的取值范围;
(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
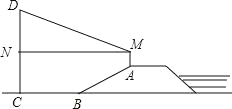
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
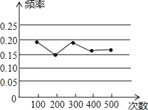
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂足为
垂足为![]() .
.
(1)填空:![]() _________°;
_________°;
(2)![]() 是线段
是线段![]() 上的动点,连结
上的动点,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,点
,点![]() 的对应点是点
的对应点是点![]() ,连接
,连接![]() ,得到
,得到![]() .
.
①如图1,若点![]() 在直线
在直线![]() 上,
上,![]() ,求
,求![]() 的值.
的值.
②连结![]() ,直线A
,直线A![]() 直线
直线![]() 是否平行,为什么?
是否平行,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连结CD交AB于点E.点P从点A出发沿AO向终点O运动,在整个运动过程中,△CEP与△DEQ的面积和的变化情况是( )

A. 一直减小 B. 一直不变
C. 先变大后变小 D. 先变小后变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)求S△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com