
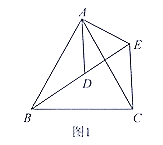
【题目】(1)问题发现:如图1, ![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接
在同一直线上,连接![]()
①求证:![]() ; ②求
; ②求![]() 的度数.
的度数.
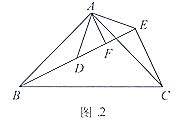
(2)拓展探究:如图2, ![]()
![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上
在同一直线上![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]()
①求![]() 的度数:
的度数:
②判断线段![]() 之间的数量关系(直接写出结果即可).
之间的数量关系(直接写出结果即可).
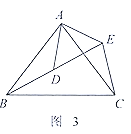
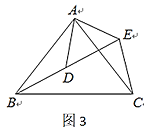
![]() 解决问题:如图3,
解决问题:如图3,![]() 和
和![]() 均为等腰三角形,
均为等腰三角形,![]() ,点
,点![]() 在同一直线上,连接
在同一直线上,连接![]() .求
.求![]() 的度数(用含
的度数(用含![]() 的代数式表示,直接写出结果即可).
的代数式表示,直接写出结果即可).
【答案】(1)①证明见解析;②60°;(2)①90°;②BE=CE+2AF;(3)∠AEC=90°+![]() .
.
【解析】
(1)根据等边三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=60°,根据SAS进一步证明△BAD≌△CAE,依据其性质可得![]() ,再根据对应角相等求出
,再根据对应角相等求出![]() 的度数;
的度数;
(2)根据等腰直角三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=90°,根据SAS进一步证明△BAD≌△CAE,根据对应角相等求出![]() 的度数;因为DE=2AF,BD=EC,结合线段的和差关系得出结论;
的度数;因为DE=2AF,BD=EC,结合线段的和差关系得出结论;
(3)根据等腰三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=n°,根据SAS进一步证明△BAD≌△CAE,根据对应角相等求出得出∠ADB=![]() 的度数,结合内角和用n表示∠ADE的度数,即可得出结论.
的度数,结合内角和用n表示∠ADE的度数,即可得出结论.
(1)①∵△ABC和△ADE均为等边三角形(如图1),
∴ AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴ ∠BAC-∠DAC=∠DAE-∠DAC,
∴ ∠BAD=∠CAE.
∴ △BAD≌△CAE(SAS)
∴ BD=CE.
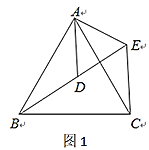
② 由△CAE≌△BAD,
∴ ∠AEC=∠ADB=180°-∠ADE=120°.
∴ ∠BEC=∠AEC-∠AED=120°-60°=60°.
(2)①∵△ABC和△ADE均为等腰直角三角形(如图2),
∴ AB=AC,AD=AE,∠ADE=∠AED=45°,
∵ ∠BAC=∠DAE=90°,
∴ ∠BAC-∠DAC=∠DAE-∠DAC,
∴ ∠BAD=∠CAE.
∴ △BAD≌△CAE(SAS).
∴ BD=CE,∠AEC=∠ADB=180°-∠ADE=135°.
∴ ∠BEC=∠AEC-∠AED=135°-45°=90°.
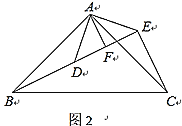
② BE=CE+2AF.
(3)如图3:∠AEC=90°+![]() ,理由如下,
,理由如下,
∵△ABC和△ADE均为等腰直角三角形,
∴ AB=AC,AD=AE,∠ADE=∠AED=n°,
∴ ∠BAC-∠DAC=∠DAE-∠DAC,
∴ ∠BAD=∠CAE.
∴ △BAD≌△CAE(SAS).
∴ ∠AEC=∠ADB=180°-∠ADE=180°-![]() .
.
∴∠AEC=90°+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
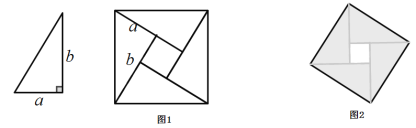
【题目】我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
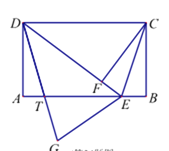
【题目】如图,在四边形ABCD中,AB∥CD,点E在AB上,AB=DC=DE, AD⊥AB,BC⊥AB,CF⊥DE,垂足分别为点A,B,F,AD=BC=6,EB=2.
(1)求证:CF=CB;
(2)求△DEC的面积S的值;
(3)若将△DEC沿着DE翻折得到△DEG,DG交AB于点T,试判断线段DT与CE的长度是否相等:并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com