
【题目】我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,求
,求![]() 的值.
的值.
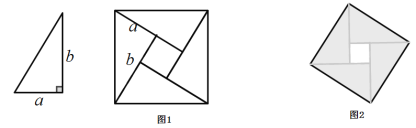
【答案】(1)见解析;(2)证明见解析;(3)25.
【解析】
(1)直接叙述勾股定理的内容,并用字母表明三边关系;
(2)利用大正方形面积、小正方形面积和4个直角三角形的面积和之间的关系列式整理即可证明;
(3)将原式利用完全平方公式展开,由勾股定理的内容可得出![]() 为大正方形面积和4个直角三角形的面积和,根据已知条件即可求得.
为大正方形面积和4个直角三角形的面积和,根据已知条件即可求得.
解:(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中,两条直角边分别为 a、b,斜边为 c,a2+b2= c2.
(2)∵ S大正方形=c2,S小正方形=(b-a)2,4 SRt△=4×![]() ab=2ab,
ab=2ab,
∴ c2=2ab+(b-a)2=2ab+b2-2ab+a2=a2+b2,
即 a2+b2= c2.
(3)∵ 4 SRt△= S大正方形- S小正方形=13-1=12,
∴ 2ab=12.
∴ (a+b)2= a2+b2+2ab=c2+2ab=13+12=25.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )

A. 12 B. 6 C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
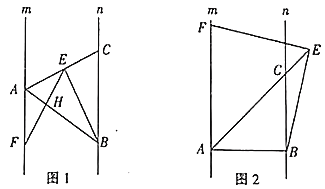
(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
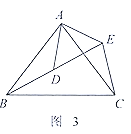
【题目】(1)问题发现:如图1, ![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接
在同一直线上,连接![]()
①求证:![]() ; ②求
; ②求![]() 的度数.
的度数.
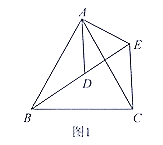
(2)拓展探究:如图2, ![]()
![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上
在同一直线上![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]()
①求![]() 的度数:
的度数:
②判断线段![]() 之间的数量关系(直接写出结果即可).
之间的数量关系(直接写出结果即可).
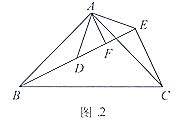
![]() 解决问题:如图3,
解决问题:如图3,![]() 和
和![]() 均为等腰三角形,
均为等腰三角形,![]() ,点
,点![]() 在同一直线上,连接
在同一直线上,连接![]() .求
.求![]() 的度数(用含
的度数(用含![]() 的代数式表示,直接写出结果即可).
的代数式表示,直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数![]() 的图像经过点E,则k的值是 ( )
的图像经过点E,则k的值是 ( )
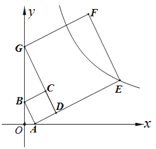
(A)33 (B)34 (C)35 (D)36
查看答案和解析>>
科目:初中数学 来源: 题型:
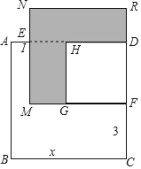
【题目】若 x 满足 (9x)(x4)=4, 求 (4x)2+(x9)2 的值.
设 9x=a,x4=b, 则 (9x)(x4)=ab=4,a+b=(9x)+(x4)=5 ,
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题:
(1)若 x 满足 (5x)(x2)=2, 求 (5x)2+(x2)2 的值
(2)已知正方形 ABCD 的边长为 x , E , F 分别是 AD 、 DC 上的点,且 AE=1 , CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
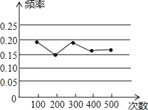
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com