
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )

A. 12 B. 6 C. 6![]() D.
D. ![]()
【答案】D
【解析】
连接B'B,利用旋转的性质和直角三角形的性质解答即可.
连接B'B,
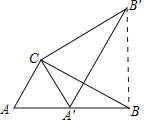
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴AC=A'C,AB=A'B,∠A=∠CA'B'=60°,
∴△AA'C是等边三角形,
∴∠AA'C=60°,
∴∠B'A'B=180°-60°-60°=60°,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴∠ACA'=∠BAB'=60°,BC=B'C,∠CB'A'=∠CBA=90°-60°=30°,
∴△BCB'是等边三角形,
∴∠CB'B=60°,
∵∠CB'A'=30°,
∴∠A'B'B=30°,
∴∠B'BA'=180°-60°-30°=90°,
∵∠ACB=90°,∠A=60°,AC=6,
∴AB=12,
∴A'B=AB-AA'=AB-AC=6,
∴B'B=6![]() ,
,
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B(m,﹣2).
的图象交于点A(1,4)和点B(m,﹣2).

(1)求一次函数的关系式;
(2)求△AOB的面积;
(3)观察图象,写出使得y1≤y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
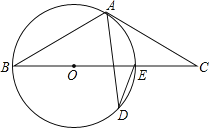
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(多选)在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离
地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系,下列说法正确的是( )
(小时)的函数关系,下列说法正确的是( )

A.甲乙两车出发2小时后相遇
B.甲车速度是40千米/小时
C.相遇时乙车距离![]() 地100千米
地100千米
D.乙车到![]() 地比甲车到
地比甲车到![]() 地早
地早![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店计划购进![]() ,
,![]() 两种笔记本共60本,每本
两种笔记本共60本,每本![]() 种笔记本比
种笔记本比![]() 种笔记本的利润高3元,销售2本
种笔记本的利润高3元,销售2本![]() 种笔记本与3本
种笔记本与3本![]() 种笔记本所得利润相同,其中
种笔记本所得利润相同,其中![]() 种笔记本的进货量不超过进货总量的
种笔记本的进货量不超过进货总量的![]() ,
,![]() 种笔记本的进货量不少于30本.
种笔记本的进货量不少于30本.
(1)每本![]() 种笔记本与
种笔记本与![]() 种笔记本的利润各为多少元?
种笔记本的利润各为多少元?
(2)设购进![]() 种笔记本
种笔记本![]() 本,销售总利润为
本,销售总利润为![]() 元,文具店应如何安排进货才能使得
元,文具店应如何安排进货才能使得![]() 最大?
最大?
(3)实际进货时,![]() 种笔记本进价下降
种笔记本进价下降![]() (
(![]() )元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
)元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
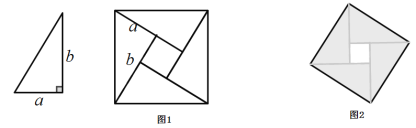
【题目】我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com