
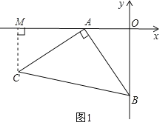
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
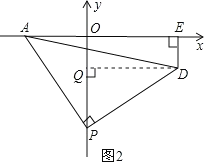
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
【答案】(1)点C的坐标为(6,2); (2) OPDE= 2; (3)结论②是正确的,m+n=4.
【解析】
(1)过C点作CM⊥x轴于M点,因为AC=AB,则作CM⊥x轴,即求CM和AM的值,容易得△MAC≌△OBA,根据已知即可求得C点的值;
(2)求OPDE的值则将其放在同一直线上,过D作DQ⊥OP于Q点,即是求PQ的值,由图易求得△AOP≌△PDQ(AAS),即可求得PQ的长;
(3)利用(2)的结论,可知m+n为定长是正确的,过F分别作x轴和y轴的垂线,类似(2),即可求得m+n的值.
(1)过C作CM⊥x轴于M点,如图1,
∵CM⊥OA,AC⊥AB,
∴∠MAC+∠OAB=![]() ,∠OAB+∠OBA=
,∠OAB+∠OBA=![]()
则∠MAC=∠OBA
在△MAC和△OBA中
则△MAC≌△OBA(AAS)
则CM=OA=2,MA=OB=4,则点C的坐标为(6,2);
(2)过D作DQ⊥OP于Q点,如图2,
则OPDE=PQ,∠APO+∠QPD=![]() ,
,
∠APO+∠OAP=![]() ,则∠QPD=∠OAP,
,则∠QPD=∠OAP,
在△AOP和△PDQ中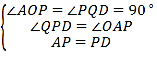
则△AOP≌△PDQ(AAS)
∴OPDE=PQ=OA=2;
(3)结论②是正确的,m+n=4,
如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,

则FS=FT=2,∠FHS=∠HFT=∠FGT,
在△FSH和△FTG中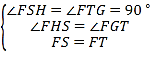
则△FSH≌△FTG(AAS)
则GT=HS,
又∵G(0,m),H(n,0),点F坐标为(2,2),
∴OT═OS=2,OG=|m|=m,OH=n,
∴GT=OGOT=m2,HS=OH+OS=n+2,
则2m=n+2,
则m+n=4.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 交于点
交于点![]() ,延长
,延长![]() 、
、![]() ,
,![]() ,
,![]() ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( )
①CP平分∠ACF; ②∠ABC+2∠APC=180°;
③∠ACB=2∠APB; ④若PM⊥BE,PN⊥BC,则AM+CN=AC;

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,雷达站C处检测到一枚由地面垂直升空的巡航导弹,导弹以240m/s的速度,用10秒从点A飞行到点B,在C处测得点A,B的仰角分别为34°和45°,求导弹发射位置O与雷达站C之间的距离(结果精确到0.1km),(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
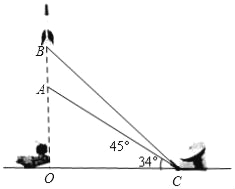
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,按以下步骤:①分别以A.B为圆心,以大于![]() AB的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D. 若AC=1.5,∠B=15°.则BD等于( )
AB的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D. 若AC=1.5,∠B=15°.则BD等于( )

A.1.5B.2C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
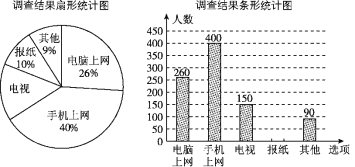
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如图所示尚不完整的统计图.
根据图中信息解答下列问题:
(1)这次接受调查的市民总人数是________;
(2)扇形统计图中,“电视”所在扇形的圆心角的度数是________;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑上网和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,∠ABC=45°,AB=BC,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.H是BC边的中点,连接DH与BE相交于点G,

(1)求证BF=AC;
(2)求证CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为_____.
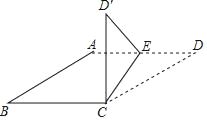
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190 m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.

⑴ 小明行走的总路程是 m,他途中休息了 min.
⑵ ①当60≤x≤90时,求y与x的函数关系式;
②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com