
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190 m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.

⑴ 小明行走的总路程是 m,他途中休息了 min.
⑵ ①当60≤x≤90时,求y与x的函数关系式;
②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
【答案】(1)3800, 30;(2)①y=60x-1600;②小明离缆车终点的路程是1200m
【解析】
(1)由函数图象可以直接得出小明行走的路程是3800米,途中休息了30分钟;(2)①设当60≤x≤90时,y与x的函数关系式为y=kx+b,由待定系数法求出其解即可;②由路程÷速度=时间就可以得出小丽到达终点的时间,将这个时间代入(2)的解析式就可以求出小明行走的路程.
解:(1)由函数图象,得
小亮行走的总路程是3800米,途中休息60-30=30分钟.
故答案为:3800,30;
(2)①设当60≤x≤90时,y与x的函数关系式为y=kx+b,
∵图象过点(60,2000),(90,3800),
∴![]() ,
,
解得![]() ,
,
∴y=60x-1600;
②∵小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min,
∴小丽行驶的路程为;3800÷2=1900m,行驶的时间为:1900÷190=10min.
∴小丽到达终点,小明行驶的时间为:60+10=70min.
∴将x=70代入y=60x-1600得,y=60×70-1600=2600.
∴小明离缆车终点的路程是:3800-2600=1200m.
答:小明离缆车终点的路程是1200m.


科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察表格,然后回答问题:

(1)表格中x= ;y= .
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;
≈ ;
②已知![]() =8.973,若
=8.973,若![]() =897.3,用含m的代数式表示b,则b= .
=897.3,用含m的代数式表示b,则b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
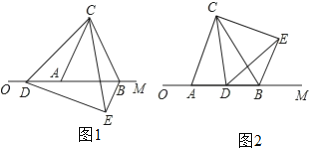
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,猜想:△CDE的形状是 三角形.
(2)请证明(1)中的猜想
(3)设OD=m,
①当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②是否存在m的值,使△DEB是直角三角形,若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ACB=90°,AC=8,BC=6,点E是AB中点,将△CAE沿着直线CE翻折,得到△CDE,连接AD,则点E到线段AD的距离等于( )

A.2B.1.8C.1.5D.1.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转得到△BA′E′,连接DA′,若∠ADC=60°,AD=5,DC=4,则DA′的大小为_____.
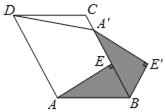
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为4 cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以每秒![]() cm的速度同时开始运动,运动过程中DE与BC相交于点P.
cm的速度同时开始运动,运动过程中DE与BC相交于点P.

(1).当点D,E运动多少秒后,△ADE为直角三角形?
(2)在点D,E运动时,线段PD与线段PE相等吗?如果相等,予以证明;如不相等,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com