
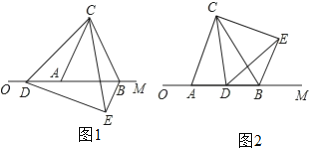
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,猜想:△CDE的形状是 三角形.
(2)请证明(1)中的猜想
(3)设OD=m,
①当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②是否存在m的值,使△DEB是直角三角形,若存在,请直接写出m的值;若不存在,请说明理由.
【答案】(1)等边;(2)详见解析;(3)①2![]() +4;②当m=2或14时,以D、E、B为顶点的三角形是直角三角形.
+4;②当m=2或14时,以D、E、B为顶点的三角形是直角三角形.
【解析】
(1)由旋转的性质猜想结论;
(2)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;
(3)①当6<m<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;
②存在,分四种情况讨论:a)当点D与点B重合时,D,B,E不能构成三角形;
b)当0≤m<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA﹣DA=6﹣4=2=m;
c)当6<m<10时,此时不存在;
d)当m>10时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到m=14.
(1)等边;
(2)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形.
(3)①存在,当6<t<10时,由旋转的性质得:BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2![]() ,∴△BDE的最小周长=CD+4=2
,∴△BDE的最小周长=CD+4=2![]() +4;
+4;
②存在,分四种情况讨论:
a)∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意;
b)当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°.
∵∠CEB=∠CDA,∴∠CDA=30°.
∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;
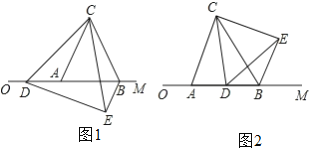
c)当6<m<10时,由∠DBE=120°>90°,∴此时不存在;
d)当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14.
综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,按以下步骤:①分别以A.B为圆心,以大于![]() AB的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D. 若AC=1.5,∠B=15°.则BD等于( )
AB的长为半径作弧,两弧相交于两点M、N;②作直线MN交BC于点D. 若AC=1.5,∠B=15°.则BD等于( )

A.1.5B.2C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
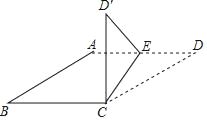
【题目】如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
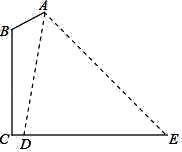
【题目】向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数且abc≠0)与直线l都经过y轴上的同一点,且抛物线的顶点在直线l上,则称抛物线L与直线l具有“一带一路”关系,并且将直线1叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=2x2﹣4x+1与直线y=nx+1具有“一带一路”关系,如图,设抛物线与x轴的一个交点为A,与y轴交于点B,其顶点为C.
①求△ABC的面积;
②在y轴上是否存在一点P,使S△PBC=![]() S△ABC,若存在,直接写出点P的坐标,若不存在,请说明理由.
S△ABC,若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190 m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.

⑴ 小明行走的总路程是 m,他途中休息了 min.
⑵ ①当60≤x≤90时,求y与x的函数关系式;
②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=5,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,当BP= 时,△ADP是等腰直角三角形.(请直接写出答案)
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并加以证明.
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,请画出图形,并求线段B′D的长度.(参考定理:若直角△ABC中,∠C是直角,则BC2+AC2=AB2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com