
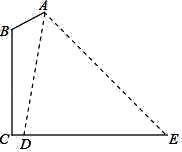
【题目】向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
【答案】灯杆AB的长度为2.8米.
【解析】
过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.设AF=x知EF=AF=x、DF=![]() =
=![]() ,由DE=13.3求得x=11.4,据此知AG=AF﹣GF=1.4,再求得∠ABG=∠ABC﹣∠CBG=30°可得AB=2AG=2.8.
,由DE=13.3求得x=11.4,据此知AG=AF﹣GF=1.4,再求得∠ABG=∠ABC﹣∠CBG=30°可得AB=2AG=2.8.
过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
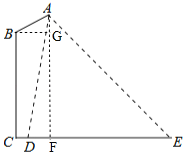
由题意得:∠ADE=α,∠E=45°.
设AF=x.
∵∠E=45°,∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF=![]() ,∴DF=
,∴DF=![]() =
=![]() .
.
∵DE=13.3,∴x+![]() =13.3,∴x=11.4,∴AG=AF﹣GF=11.4﹣10=1.4.
=13.3,∴x=11.4,∴AG=AF﹣GF=11.4﹣10=1.4.
∵∠ABC=120°,∴∠ABG=∠ABC﹣∠CBG=120°﹣90°=30°,∴AB=2AG=2.8.
答:灯杆AB的长度为2.8米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
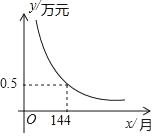
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
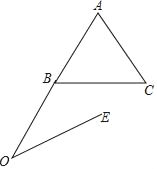
【题目】如图,等边△ABC中,AB=3,点O在AB的延长线上,OA=6,且∠AOE=30°,动点P从点O出发,以每秒![]() 个单位的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从点B出发,以每秒1个单位的速度沿折线B…C…A向点A运动,Q与A重合时,P、Q同时停止运动,设P的运动时间为t秒.
个单位的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从点B出发,以每秒1个单位的速度沿折线B…C…A向点A运动,Q与A重合时,P、Q同时停止运动,设P的运动时间为t秒.
(1)当△POB是直角三角形时,求t的值;
(2)当⊙P过点C时,求⊙P与线段OA围成的封闭图形的面积;
(3)当⊙P与△ABC的边所在直线相切时,求t的值;
(4)当线段OQ与⊙P只有一个公共点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察表格,然后回答问题:

(1)表格中x= ;y= .
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;
≈ ;
②已知![]() =8.973,若
=8.973,若![]() =897.3,用含m的代数式表示b,则b= .
=897.3,用含m的代数式表示b,则b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
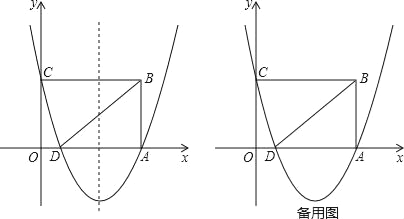
【题目】如图,在平面直角坐标系中,点O是原点,矩形OABC的顶点A在x轴的正半轴上,顶点C在y的正半轴上,点B的坐标是(5,3),抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一点,以M、B、D为顶点的三角形的面积是6,求点M的坐标;
(3)点P从点D出发,以每秒1个单位长度的速度沿D→B匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度沿B→A→D匀速运动,当点P到达点B时,P、Q同时停止运动,设运动的时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是等腰三角形?请直接写出所有符合条件的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
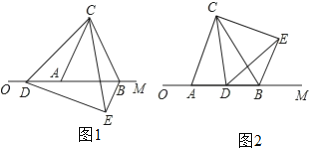
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,猜想:△CDE的形状是 三角形.
(2)请证明(1)中的猜想
(3)设OD=m,
①当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②是否存在m的值,使△DEB是直角三角形,若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ACB=90°,AC=8,BC=6,点E是AB中点,将△CAE沿着直线CE翻折,得到△CDE,连接AD,则点E到线段AD的距离等于( )

A.2B.1.8C.1.5D.1.4
查看答案和解析>>
科目:初中数学 来源: 题型:
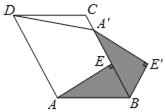
【题目】如图,已知在ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转得到△BA′E′,连接DA′,若∠ADC=60°,AD=5,DC=4,则DA′的大小为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.

(1)利用尺规完成以下作图,并保留作图痕迹(不写做法)
①在射线BM上作一点C,使AC=AB,连接AC
②作∠ABM的角平分线交AC于点D
③在射线CM上作一点E,使CE=CD,连接DE
(2)在(1)中所作的图形中,通过观察和测量可以发现BD=DE,请将下面的证明过程补充完整证明:∵AC=AB,
∴∠ =∠
∵BD平分∠ABM,
∴∠DBE=﹣![]() ∠
∠
∵CE=CD
∴∠CDE=∠CED
∴∠ACB=∠CDE+∠CED,
∴∠CED=![]() ∠ACB
∠ACB
∴∠DBE=∠CED,
∴BD=DE,( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com