
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=5,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,当BP= 时,△ADP是等腰直角三角形.(请直接写出答案)
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并加以证明.
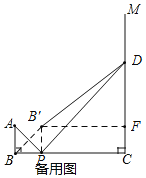
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,请画出图形,并求线段B′D的长度.(参考定理:若直角△ABC中,∠C是直角,则BC2+AC2=AB2)
【答案】(1)4;
(2)PB和PC的数量关系:PB=PC,证明见解析;
(3)线段B′D的长度为5.
【解析】
(1)若△ADP是等腰直角三角形.则AP=DP,必须要求△APB≌△PDC,则![]() ,所以BP=4;
,所以BP=4;
(2)延长线段AP、DC交于点E,则△DPA≌△DPE,PA=PE,进一步可证明△APB≌△EPC,则PB=PC;
(3)先按要求作出图形,然后将B′D放在直角三角形中,利用勾股定理求出B′D的长度.
解:(1)当BP=4时,CP=BC﹣BP=5=4=1,
∵AB=1,
∴AB=PC,
∵AB⊥BC,DP⊥AP,CM⊥BC,
∴∠B=∠C=90°,∠APB+∠DPC=90°=∠PDC+∠DPC,
∴∠APB=∠PDC,
在△APB和△PDC中,
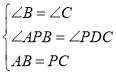
∴△APB≌△PDC(AAS),
∴AP=DP,
又∵∠APD=90°,
∴△ADP是等腰直角三角形,
故答案为:4;
(2)PB和PC的数量关系:PB=PC,
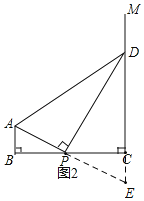
证明:如图2,延长线段AP、DC交于点E,
∵DP平分∠ADC,
∴∠ADP=∠EDP.
∵DP⊥AP,
∴∠DPA=∠DPE=90°.
在△DPA和△DPE中,

∴△DPA≌△DPE(ASA),
∴PA=PE.
∵AB⊥BP,CM⊥CP,
∴∠ABP=∠ECP=90°.
在△APB和△EPC中,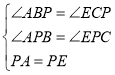
∴△APB≌△EPC(AAS),
∴PB=PC;
(3)如图,连接B'P,过点B'作B'F⊥CD于F,则∠B'FC=∠C=90°,
∵△PDC是等腰三角形,
∴△PCD为等腰直角三角形,即∠DPC=45°,
又∵DP⊥AP,
∴∠APB=45°,
∵点B关于AP的对称点为点B′,
∴∠BPB'=90°,∠APB=45°,BP=B'P,
∴△ABP为等腰直角三角形,四边形B'PCF是矩形,
∴BP=AB=1=B'P,PC=5=1=4=B'F,CF=B'P=1,
∴B'F=4,DF=4﹣1=3,
∴Rt△B'FD中,B'D=![]() =5,
=5,
故线段B′D的长度为5.


科目:初中数学 来源: 题型:
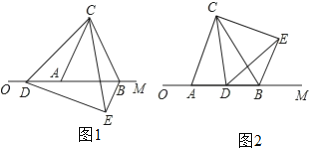
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,猜想:△CDE的形状是 三角形.
(2)请证明(1)中的猜想
(3)设OD=m,
①当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②是否存在m的值,使△DEB是直角三角形,若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为4 cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以每秒![]() cm的速度同时开始运动,运动过程中DE与BC相交于点P.
cm的速度同时开始运动,运动过程中DE与BC相交于点P.

(1).当点D,E运动多少秒后,△ADE为直角三角形?
(2)在点D,E运动时,线段PD与线段PE相等吗?如果相等,予以证明;如不相等,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠ECF=∠BCD=90°,CE=CF=5,BC=7,BD平分∠ABC,E是△BCD内一点,F是四边形ABCD外一点.(E可以在△BCD的边上)
(1)求证:DC=BC;
(2)当∠BEC=135°,设BE=a,DE=b,求a与b满足的关系式;
(3)当E落在线段BD上时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.

(1)利用尺规完成以下作图,并保留作图痕迹(不写做法)
①在射线BM上作一点C,使AC=AB,连接AC
②作∠ABM的角平分线交AC于点D
③在射线CM上作一点E,使CE=CD,连接DE
(2)在(1)中所作的图形中,通过观察和测量可以发现BD=DE,请将下面的证明过程补充完整证明:∵AC=AB,
∴∠ =∠
∵BD平分∠ABM,
∴∠DBE=﹣![]() ∠
∠
∵CE=CD
∴∠CDE=∠CED
∴∠ACB=∠CDE+∠CED,
∴∠CED=![]() ∠ACB
∠ACB
∴∠DBE=∠CED,
∴BD=DE,( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
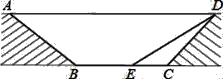
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com