
【题目】等边三角形ABC的边长为4 cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以每秒![]() cm的速度同时开始运动,运动过程中DE与BC相交于点P.
cm的速度同时开始运动,运动过程中DE与BC相交于点P.

(1).当点D,E运动多少秒后,△ADE为直角三角形?
(2)在点D,E运动时,线段PD与线段PE相等吗?如果相等,予以证明;如不相等,说明理由.
【答案】(1)![]() ;(2)相等,证明见解析.
;(2)相等,证明见解析.
【解析】
(1)设当点D,E运动![]() 秒后,△ADE为直角三角形,则
秒后,△ADE为直角三角形,则![]() ,
,![]() ,
,![]() ,
,![]() ,根据30°角的直角边=斜边的一半建立方程,求出其解即可;
,根据30°角的直角边=斜边的一半建立方程,求出其解即可;
(2)作DG∥AB交BC于点E,证明△DGP≌△EBP,就可以得出PD=PE.
解:(1)∵△ABC是等边三角形,
∴AB=BC=AC=4cm,∠A=∠ABC=∠C=60°.
设当点D,E运动![]() 秒后,△ADE为直角三角形,
秒后,△ADE为直角三角形,
∴∠ADE=90°,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴∠AED=30°,
∴AE=2AD,
∴![]() ,
,
解得:![]() ;
;
答:当点D,E运动![]() 秒后,△ADE为直角三角形运动;
秒后,△ADE为直角三角形运动;
(2)线段PD与线段PE相等,证明如下:
证明:作DG∥AB交BC于点G,
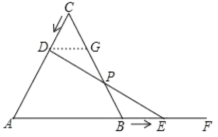
∴∠GDP=∠BEP,∠DGP=∠EBP,∠CDG=∠A=60°,∠CGD=∠ABC=60°,
∴∠C=∠CDG=∠CGD,
∴△CDG是等边三角形,
∴DG=DC,
∵DC=BE,
∴DG=BE.
在△DGP和△EBP中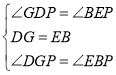 ,
,
∴△DGP≌△EBP(ASA),
∴PD=PE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
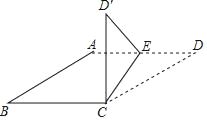
【题目】如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190 m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.

⑴ 小明行走的总路程是 m,他途中休息了 min.
⑵ ①当60≤x≤90时,求y与x的函数关系式;
②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
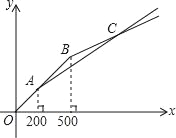
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() ,以下结论:①抛物线交
,以下结论:①抛物线交![]() 轴有两个不同的交点;②不论
轴有两个不同的交点;②不论![]() 取何值,抛物线总是经过一个定点;③设抛物线交
取何值,抛物线总是经过一个定点;③设抛物线交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() ,则
,则![]() ;④抛物线的顶点在
;④抛物线的顶点在![]() 图象上;⑤抛物线交
图象上;⑤抛物线交![]() 轴于
轴于![]() 点,若
点,若![]() 是等腰三角形,则
是等腰三角形,则![]() ,
,![]() ,
,![]() .其中正确的序号是( )
.其中正确的序号是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或解方程
(1)2![]() ﹣3
﹣3![]() +
+![]()
(2)(![]() ﹣2)(
﹣2)(![]() +2)﹣(
+2)﹣(![]() )2
)2
(3)(﹣3)0﹣![]() ﹣|1﹣
﹣|1﹣![]() |﹣
|﹣![]()
(4)3(3x﹣1)2﹣27=0
(5)![]() =﹣2
=﹣2
(6)![]() x﹣2=
x﹣2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=5,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,当BP= 时,△ADP是等腰直角三角形.(请直接写出答案)
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并加以证明.
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,请画出图形,并求线段B′D的长度.(参考定理:若直角△ABC中,∠C是直角,则BC2+AC2=AB2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com