
【题目】关于二次函数![]() ,以下结论:①抛物线交
,以下结论:①抛物线交![]() 轴有两个不同的交点;②不论
轴有两个不同的交点;②不论![]() 取何值,抛物线总是经过一个定点;③设抛物线交
取何值,抛物线总是经过一个定点;③设抛物线交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() ,则
,则![]() ;④抛物线的顶点在
;④抛物线的顶点在![]() 图象上;⑤抛物线交
图象上;⑤抛物线交![]() 轴于
轴于![]() 点,若
点,若![]() 是等腰三角形,则
是等腰三角形,则![]() ,
,![]() ,
,![]() .其中正确的序号是( )
.其中正确的序号是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
【答案】D
【解析】
令![]() ,利用该一元二次方程的△即可判断①的正误;当x=1时,方程中变化的参数k会被“抵消”,则抛物线总是会经过一个定点,由此判断②;可直接代入k=4来验证③;求出
,利用该一元二次方程的△即可判断①的正误;当x=1时,方程中变化的参数k会被“抵消”,则抛物线总是会经过一个定点,由此判断②;可直接代入k=4来验证③;求出![]() 顶点坐标,然后代入
顶点坐标,然后代入![]() ,来判断④;可采取直接代入进行验证,选择较容易的0和1先代入,当k=1时,
,来判断④;可采取直接代入进行验证,选择较容易的0和1先代入,当k=1时,![]() 不是等腰三角形.
不是等腰三角形.
解:△=k2-4k+4=(k-2)2≥0,当k=2时,抛物线与x轴只有1个交点,①错误;
当x=1时,y=1-k+k-1=0,即抛物线过定点(1,0),②正确;
当k=4时,y=x2-4x+3,则抛物线与x轴的交点为:x2-4x+3=0,解得x1=3,x2=1,则AB=3-1=2,故③错误;
二次函数![]() 的顶点为(
的顶点为(![]() ,
,![]() ),代入
),代入![]() 进行验证:
进行验证:
当x=![]() 时,
时,![]() ,故④正确;
,故④正确;
当k=1时,![]() ,解得抛物线与x轴的两个交点为:(0,0)、(1,0),此时
,解得抛物线与x轴的两个交点为:(0,0)、(1,0),此时![]() 不是等腰三角形,故⑤错误.
不是等腰三角形,故⑤错误.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知y﹣3与3x+2正比例,且x=2时,y=5
(1)求y与x之间的函数关系式,并指出它是什么函数;
(2)点(4,6)是否在这个函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建成学校举行美化绿化校园活动,九年级计划购买![]() ,
,![]() 两种花木共100棵绿化操场,其中
两种花木共100棵绿化操场,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若购进![]() ,
,![]() 两种花木刚好用去8000元,则购买了
两种花木刚好用去8000元,则购买了![]() 两种花木各多少棵?
两种花木各多少棵?
(2)如果购买![]() 花木的数量不少于
花木的数量不少于![]() 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为4 cm,点D从点C出发沿CA向点A运动,点E从点B出发沿AB的延长线BF向右运动,已知点D,E都以每秒![]() cm的速度同时开始运动,运动过程中DE与BC相交于点P.
cm的速度同时开始运动,运动过程中DE与BC相交于点P.

(1).当点D,E运动多少秒后,△ADE为直角三角形?
(2)在点D,E运动时,线段PD与线段PE相等吗?如果相等,予以证明;如不相等,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠ECF=∠BCD=90°,CE=CF=5,BC=7,BD平分∠ABC,E是△BCD内一点,F是四边形ABCD外一点.(E可以在△BCD的边上)
(1)求证:DC=BC;
(2)当∠BEC=135°,设BE=a,DE=b,求a与b满足的关系式;
(3)当E落在线段BD上时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
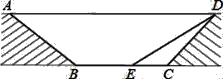
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com