
����Ŀ��Ϊ���⽻ͨӵ�£�ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ��ͼ�е���AD��ͨ��BCƽ�У�ͨ��ˮƽ����BCΪ8�ף���BCD=135����ͨ��б��CD�ij�Ϊ6�ף�ͨ��б��AB���¶�i=1��![]() ��
��
��1����ͨ��б��AB�ij���
��2��Ϊ�����������ߵ����ʶȣ��⽫���ͼ�е�ͨ��б��CD���¶ȱ仺���ĺ��ͨ��б��DE���½�Ϊ30�������ʱBE�ij���
���𰸾���ȷ��0.1�ף��ο����ݣ�![]() ��1.41��
��1.41��![]() ��2.24��
��2.24��![]() ��2.45��
��2.45��
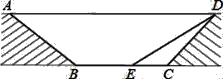
���𰸡���1��ͨ��б��AB�ij�ԼΪ7.4�ף���2��BE�ij�ԼΪ4.9�ף�
��������
��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M���ٸ��ݡ�BCD=135����ͨ��б��CD�ij�Ϊ6�ף��Ϳ��Եó�ͨ���ĸ߶�DM��AN=DM���ٸ���ͨ��б��AB���¶�i=1��![]() ���Ϳ������ͨ��б��AB�ij�����2���ĺ��ͨ��б��DE���½�Ϊ30����DM�߶ȿ������EM���ȣ�EC=EM-CM��BE=BC-EC���ɵó���
���Ϳ������ͨ��б��AB�ij�����2���ĺ��ͨ��б��DE���½�Ϊ30����DM�߶ȿ������EM���ȣ�EC=EM-CM��BE=BC-EC���ɵó���
��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��
�ߡ�BCD=135�㣬
���DCM=45�㣮
����Rt��CMD�У���CMD=90�㣬CD=6��
��DM=CM=![]() CD=3
CD=3![]() ��
��
��AN=DM=3![]() ��
��
��ͨ��б��AB���¶�i=1��![]() ��
��
��tan��ABN=![]() =
=![]() ��
��
��BN=![]() AN=6��
AN=6��
��AB=![]() =3
=3![]() ��7.4��
��7.4��
��ͨ��б��AB�ij�ԼΪ7.4�ף�
��2������Rt��MED�У���EMD=90�㣬��DEM=30�㣬DM=3![]() ��
��
��EM=![]() DM=3
DM=3![]() ��
��
��EC=EM��CM=3![]() ��3
��3![]() ��
��
��BE=BC��EC=8����3![]() ��3
��3![]() ��=8+3
��=8+3![]() ��3
��3![]() ��4.9��
��4.9��
����ʱBE�ij�ԼΪ4.9�ף�


 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������L��y=ax2+bx+c��a��b��c�dz�����abc��0����ֱ��l������y���ϵ�ͬһ�㣬�������ߵĶ�����ֱ��l�ϣ����������L��ֱ��l������һ��һ·����ϵ�����ҽ�ֱ��1����������L����·������������L����ֱ��l����������
��1������·����l�ı���ʽΪy=2x��4��������������L�Ķ���ĺ�����Ϊ��1������������L�ı���ʽ��
��2�����������y=2x2��4x+1��ֱ��y=nx+1������һ��һ·����ϵ����ͼ������������x���һ������ΪA����y�ύ�ڵ�B���䶥��ΪC��
������ABC�������
����y�����Ƿ����һ��P��ʹS��PBC=![]() S��ABC�������ڣ�ֱ��д����P�����꣬�������ڣ���˵�����ɣ�
S��ABC�������ڣ�ֱ��д����P�����꣬�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���![]() �����½��ۣ��������߽�
�����½��ۣ��������߽�![]() ����������ͬ�Ľ��㣻�ڲ���
����������ͬ�Ľ��㣻�ڲ���![]() ȡ��ֵ�����������Ǿ���һ�����㣻���������߽�
ȡ��ֵ�����������Ǿ���һ�����㣻���������߽�![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ����
����![]() ���������ߵĶ�����
���������ߵĶ�����![]() ͼ���ϣ��������߽�
ͼ���ϣ��������߽�![]() ����
����![]() �㣬��
�㣬��![]() �ǵ��������Σ���
�ǵ��������Σ���![]() ��
��![]() ��
��![]() ��������ȷ������ǣ� ��
��������ȷ������ǣ� ��
A. �٢ڢ� B. �ڢۢ� C. �٢ܢ� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����![]() �ĶԳ���
�ĶԳ���![]() ���ҵ�
���ҵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ��Ϊ���������Σ������������ĵ�
��Ϊ���������Σ������������ĵ�![]() ��_________��.
��_________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��BC������CM��BC����BC��5��AB��1����P���߶�BC �������B��C�غϣ��ϵĶ��㣬����P��DP��AP������CM�ڵ�D������AD��

��1����ͼ1����BP���� ��ʱ����ADP�ǵ���ֱ�������Σ�����ֱ��д���𰸣�
��2����ͼ2����DPƽ�֡�ADC���Բ²�PB��PC��������ϵ��������֤����
��3������PDC�ǵ��������Σ�����B����AP�ĶԳƵ�B��������B��D���뻭��ͼ�Σ������߶�B��D�ij��ȣ����ο���������ֱ�ǡ�ABC�У���C��ֱ�ǣ���BC2+AC2��AB2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
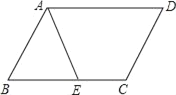
����Ŀ����ͼ����ABCD�У�AEƽ����BAD����BC�ڵ�E��
��1����AD��������F��ʹ��F��CD��BC�ľ�����ȣ�
��Ҫ�߹���ͼ��������ͼ�ۼ�����д������
��2���ж��ı���AECF��ʲô�����ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
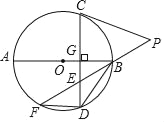
����Ŀ����ͼ��ABΪ��O��ֱ����CD��AB�ڵ�G��E��CD��һ�㣬��BE=DE���ӳ�EB����P������CP��ʹPC=PE���ӳ�BE����O���ڵ�F������BD��FD��
��1����֤��CD=BF��
��2����֤��PC����O�����ߣ�
��3����tanF=![]() ��AG��BG=
��AG��BG=![]() ����ED��ֵ��
����ED��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON=90��������ABCD�Ķ���A��B�ֱ��ڱ�OM��ON�ϣ���B�ڱ�ON���˶�ʱ��A��֮��OM���˶�������ABCD����״���ֲ��䣬����AB=2��BC=1���˶������У���D����O��������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����DE��AC��CE��BD����AC��2�����ı���OCED���ܳ�Ϊ�� ��

A.16B.8C.4D.2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com