
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
【答案】D
【解析】
根据方程有两个相等的实数根可得出b=a+1或b=-(a+1),当b=a+1时,-1是方程x2+bx+a=0的根;当b=-(a+1)时,1是方程x2+bx+a=0的根.再结合a+1≠-(a+1),可得出1和-1不都是关于x的方程x2+bx+a=0的根.
∵关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,
∴![]() ,
,
∴b=a+1或b=-(a+1).
当b=a+1时,有a-b+1=0,此时-1是方程x2+bx+a=0的根;
当b=-(a+1)时,有a+b+1=0,此时1是方程x2+bx+a=0的根.
∵a+1≠0,
∴a+1≠-(a+1),
∴1和-1不都是关于x的方程x2+bx+a=0的根.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:在直角三角形中至少有一个角不大于45°.
已知:如图所示,△ABC中,∠C=90°,求证:∠A,∠B中至少有一个不大于45°.
证明:假设__________,则∠A__________45°,∠B______45°. ∴∠A+∠B+∠C>45°+ _______+__________,这与________________________相矛盾. 所以___________不能成立,所以∠A,∠B中至少有一个角不大于45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y=k1x+4与直线l2:y=k2x﹣5交于点A,它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点,则线段EF的长度为 . 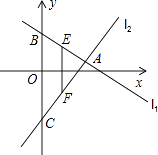
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题: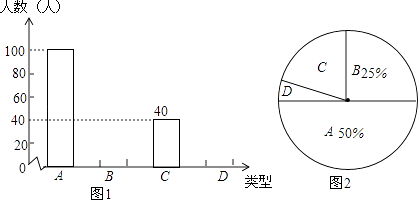
(1)此次抽样调查中,共调查了名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )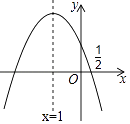
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
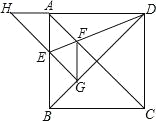
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com