
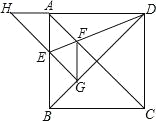
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
A. ①②③④ B. ①②③ C. ①② D. ②
【答案】B
【解析】
首先证明△ADE≌△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.
解:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DGH是由△DCB旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在Rt△AED和Rt△GED中,
![]()
∴△AED≌△GED,故②正确,
∴∠ADE=∠EDG=22.5°,AE=GE,
∴∠AED=∠AFE=67.5°,
∴AE=AF,同理GE=GF,
∴AE=GE=GF=AF,
∴四边形AEGF是菱形,故①正确,
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确.
∵AE=FG=EG=BG,BE=![]() AE,
AE,
∴BE>AE,
∴AE<![]() ,
,
∴CB+FG<1.5,故④错误.
故选:B


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
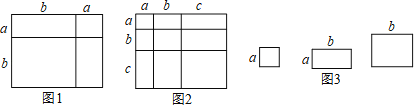
(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
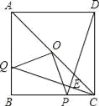
【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 以
以![]() 的速度从点
的速度从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动.
运动.
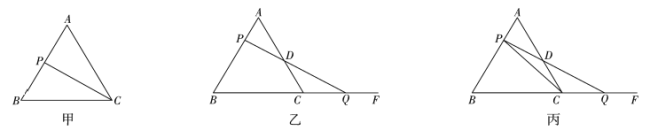
(1)如图甲,设点![]() 的运动时间为
的运动时间为![]() ,那么
,那么![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(2)若另一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,连接
方向运动,连接![]() 交
交![]() 于点
于点![]() ,如果动点
,如果动点![]() 都以
都以![]() 的速度同时出发.
的速度同时出发.
①如图乙,设运动时间为![]() ,那么
,那么![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?
②如图丙,连接![]() ,请你猜想:在点
,请你猜想:在点![]() 的运动过程中,
的运动过程中,![]() 和
和![]() 的面积有什么关系?并说明理由.
的面积有什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图.
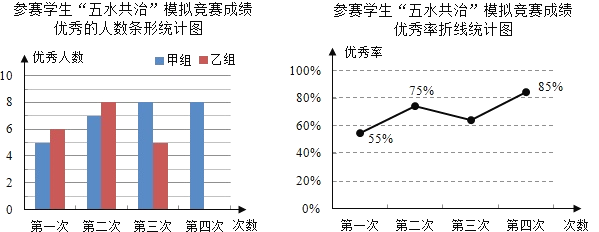
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数![]() ,方差
,方差![]() ,请通过计算说明那一组成绩优秀的人数较稳定?
,请通过计算说明那一组成绩优秀的人数较稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com