
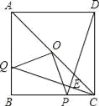
【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据正方形的性质和DP⊥CQ于点E可以得到证明△BCQ≌△CDP的全等条件;
(2)根据(1)得到BQ=PC,然后连接OB,根据正方形的性质可以得到证明△BOQ≌△COP的全等条件,然后利用全等三角形的性质就可以解决题目的问题.
证明:(1)∵四边形ABCD是正方形,
∴∠B=∠PCD=90°,BC=CD,
∴∠2+∠3=90°,
又∵DP⊥CQ,
∴∠2+∠1=90°,
∴∠1=∠3,
在△BCQ和△CDP中,
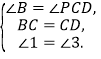
∴△BCQ≌△CDP;
(2)连接OB,
由(1)△BCQ≌△CDP可知:BQ=PC,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵点O是AC中点,
∴BO=![]() AC=CO,∠4=
AC=CO,∠4=![]() ∠ABC=45°=∠PCO,
∠ABC=45°=∠PCO,
在△BOQ和△COP中,
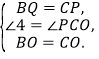
∴△BOQ≌△COP,
∴OQ=OP.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )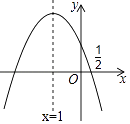
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将![]() 向右平移
向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度,得到
个单位长度,得到![]()
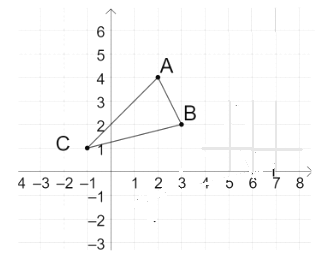
(1)在平面直角坐标系中,画出![]() ;
;
(2)写出平移后点的坐标:![]() (_____,____).
(_____,____).![]() (_____,_____).
(_____,_____).![]() (_____,_____);
(_____,_____);
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
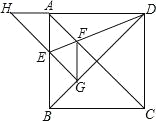
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
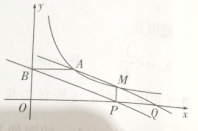
【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y=![]() (x>0)的图像上,
(x>0)的图像上,
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com