
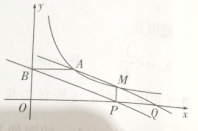
【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y=![]() (x>0)的图像上,
(x>0)的图像上,
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
【答案】(1)k=6,直线AM的解析式为![]() ;(2)详见解析;(3)能,当
;(2)详见解析;(3)能,当![]() 时,四边形ABPQ是菱形.
时,四边形ABPQ是菱形.
【解析】
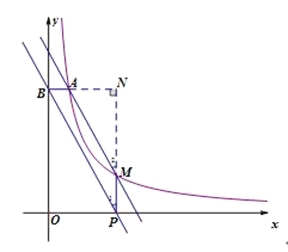
试题(1)将A坐标代入反比例解析式求出k的值即可;由k的值可得反比例解析式,将m=4代入反比例解析式求出n的值,从而确定M坐标,由待定系数法即可求出直线AM解析式;(2)如图,延长BA、PM相交于N.则∠N=90°,由A(3,2),M(m,n)可得B(0,2),P(m,0),N(m,2).又因点M(m,n)都在反比例函数![]() 的图像上,所以
的图像上,所以![]() ,利用三角函数可得
,利用三角函数可得![]() ,
,![]() ,所以
,所以![]() ,即∠1=∠2,根据同位角相等两直线平行即可得AM∥BP,再由AB∥PQ即可判定四边形ABPQ是平行四边形;(3)当四边形ABPQ是菱形时,PB=AB=3,在直角三角形BOP中,由勾股定理可列方程
,即∠1=∠2,根据同位角相等两直线平行即可得AM∥BP,再由AB∥PQ即可判定四边形ABPQ是平行四边形;(3)当四边形ABPQ是菱形时,PB=AB=3,在直角三角形BOP中,由勾股定理可列方程![]() ,解得m的值即可.
,解得m的值即可.
试题解析:(1)点A(3,2)在反比例函数![]() 的图像上
的图像上
所以![]()
当m=4时,则n=![]() ,所以M(4,
,所以M(4,![]() )
)
设直线AM的解析式为![]()
则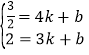
解得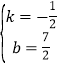
所以直线AM的解析式为![]()
(2)延长BA、PM相交于N.则∠N=90°
∵A(3,2),M(m,n)
∴B(0,2),P(m,0),N(m,2)
∴BN=m,PN=2,AN=m-3,MN=2-n
∴![]()
![]()
∴![]()
∴∠1=∠2
∴AM∥BP
∵AB∥PQ
∴四边形ABPQ是平行四边形
(3)能.当四边形ABPQ是菱形时,PB=AB=3,在直角三角形BOP中,∵![]()
∴![]()
∴![]()
∴当![]() 时,四边形ABPQ是菱形.
时,四边形ABPQ是菱形.


科目:初中数学 来源: 题型:
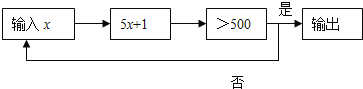
【题目】按下面程序计算,即根据输入的![]() 判断
判断![]() 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的![]() 的值作为新的
的值作为新的![]() 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入![]() 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有![]() 的值是__.
的值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A、B、C在同一条直线上,点M为线段AC的中点、点N为线段BC的中点.
(1)如图,当点C在线段AB上时:
①若线段![]() ,求
,求![]() 的长度.
的长度.
②若AB=a,求MN的长度.
(2)若![]() ,求MN的长度(用含
,求MN的长度(用含![]() 的代数式表示).
的代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学知识伴随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始资料,古巴比伦楔形文字泥板书就是其中之一,古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式:
![]() …①
…①
![]() …②
…②
(1)材料中,公式②中的空缺部分应该是 ;
(2)请你验证材料中的公式①;
(3)当![]() ,
,![]() 时,利用公式①计算
时,利用公式①计算![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
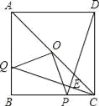
【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.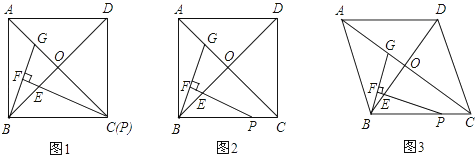
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: ![]() 与
与 ![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
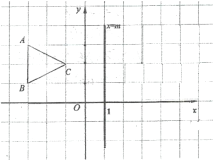
【题目】如图,在平面直角坐标系中,有△ABC和x=m直线.
(1)若A(-3,3),B (-3,1),C (-1,2),当m=1时,在图中作出△ABC关于直线x=m对称的图形,并直接写出![]() ,
,![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)若又有点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,那么
对称,那么![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 之间有什么数量关系?(直接写出答案即可)
之间有什么数量关系?(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点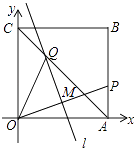
(Ⅰ)若点P的坐标为(1, ![]() ),求点M的坐标;
),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com