【题目】如图，已知直线l1：y=k1x+4与直线l2：y=k2x﹣5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB、AC的中点，则线段EF的长度为 ．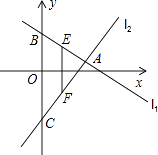 
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】疫情期间，为减少交叉感染，催生了以智能技术为支撑的无接触服务．某快递公司准备购进
，
两种型号的智能机器人送快递．经市场调査发现，型号机器人的单价比型号机器人贵600元，3台型号机器人比2台型号机器人贵1200元．
（1）求，两种型号机器人的单价各是多少元？
（2）若该快递公司准备用不超过132000元购进，两种型号机器人共50台，请问该快递公司最多可购进型号机器人多少台？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠A=90°， D是AB边上一点，且DB=DC，过BC上一点P（不包括B，C二点）作PE⊥AB，垂足为点E， PF⊥CD，垂足为点F，已知AD：DB=1：4，BC=
，求PE+PF的长.
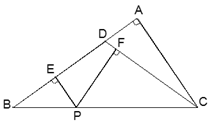
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：
某商场用8万元购进一批新款衬衫，上架后很快销售一空，商场又紧急购进第二批这种衬衫，数量是第一次的2倍，但进价涨了4元/件，结果共用去17.6万元．
（1）该商场第一批购进衬衫多少件？
（2）商场销售这种衬衫时，每件定价都是58元，剩至150件时按八折出售，全部售完．售完这两批衬衫，商场共盈利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AC=BC，D是BC上的一点，且满足∠BAD= 
∠C，以AD为直径的⊙O与AB，AC分别相交于点E，F．
（1）求证：直线BC是⊙O的切线；
（2）连接EF，若tan∠AEF= 
，AD=4，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，下列判断正确的是（ ）
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目：初中数学 来源： 题型：
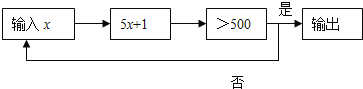
【题目】按下面程序计算，即根据输入的
判断
是否大于500，若大于500则输出，结束计算，若不大于500，则以现在的的值作为新的的值，继续运算，循环往复，直至输出结果为止．若开始输入的值为正整数，最后输出的结果为656，则满足条件的所有的值是__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ACDE是证明勾股定理时用到的一个图形，a、b、c是Rt△ABC和Rt△BED边长，易知AE=
c，这时我们把关于x的形如ax+
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题：
写出一个“勾系一元二次方程”；
求证：关于x的“勾系一元二次方程”ax+
cx+b=0必有实数根；
若x=1是“勾系一元二次方程”ax+
cx+b=0的一个根，且四边形ACDE的周长是
，求△ABC面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，函数 y kx 与 y 
的图象交于 A、B 两点，过 A 作 y 轴的垂线，交函数
的图象于点 C，连接 BC，则△ABC 的面积为（ ）
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
