练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】疫情期间，为减少交叉感染，催生了以智能技术为支撑的无接触服务．某快递公司准备购进，两种型号的智能机器人送快递．经市场调査发现，型号机器人的单价比型号机器人贵600元，3台型号机器人比2台型号机器人贵1200元．

    （1）求，两种型号机器人的单价各是多少元？

    （2）若该快递公司准备用不超过132000元购进，两种型号机器人共50台，请问该快递公司最多可购进型号机器人多少台？

    【答案】（1），两种型号机器人的单价分别是3000元，2400元；（2）该快递公司最多可购进型号机器人20台

    【解析】

    （1）设型号机器人单价为元，型号机器人单价为元，列方程组解答；

    （2）（2）设该快递公司购进型号机器人台，依据费用不超过132000元列不等式求出答案.

    解：（1）设型号机器人单价为元，型号机器人单价为元，

    根据题意，有，

    解这个方程组，得，

    答：，两种型号机器人的单价分别是3000元，2400元．

    （2）设该快递公司购进型号机器人台，根据题意，有

    ．

    解这个不等式，得．

    答：该快递公司最多可购进型号机器人20台．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数y= 的图象，当x取1，2，3，…n时，对应在反比例图象上的点分别为M1、M2、M3…Mn ， 则 + +… = ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形ABCD的对角线AC，BD交于点O，点E，F分别是OB，OC上的动点．当动点E，F满足BE＝CF时．

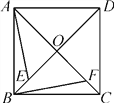
    (1)写出所有以点E或F为顶点的全等三角形；(不得添加辅助线)

    (2)求证：AE⊥BF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠C=90°，AC=BC=2，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S1；取BE中点E1 ， 作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1 ， 它的面积记作S2 ， 照此规律作下去，则S1= ， S2017= ．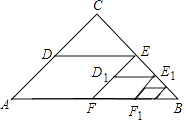

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=4x与反比例函数y= （k≠0）相交与点A（1，a），B是反比例函数图象上一点，直线OB与x轴的夹角为α，且tanα= ．

    （1）求k的值．
    （2）求点B的坐标．
    （3）设点P点在y轴上，若△PAB是以AB为直角边的直角三角形，则点P的坐标为： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边△CDE，使点E、A在直线DC的同侧，连接AE，判断AE与BC的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE．

    （1）求证：△ACD≌△BCE；

    （2）延长BE至Q，P为BQ上一点，连接CP、CQ使CP=CQ=5，若BC=8时，求PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

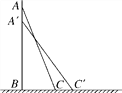
    【题目】如图，一架梯子AC长2.5米，斜靠在一面墙上，梯子底端离墙0.7米．

    (1)这个梯子的顶端距地面有多高？

    (2)如果梯子的顶端下滑了0.4米到A′，那么梯子的底端在水平方向滑动了几米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线l1：y=k1x+4与直线l2：y=k2x﹣5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB、AC的中点，则线段EF的长度为 ．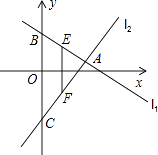

    查看答案和解析>>

    同步练习册答案