
【题目】如图,已知正方形ABCD的对角线AC,BD交于点O,点E,F分别是OB,OC上的动点.当动点E,F满足BE=CF时.
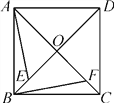
(1)写出所有以点E或F为顶点的全等三角形;(不得添加辅助线)
(2)求证:AE⊥BF.
【答案】(1) △ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;(2)见解析
【解析】试题分析:
(1)由已知条件易得AB=BC,∠ABE=∠CBF=45°,结合BE=CF可得△ABE≌△BCF;由此可得∠AEB=∠CFB,从而可得∠AEO=∠BFO,结合∠AOE=∠BOF=90°及OA=OB可得△AOE≌△BOF;由∠ADE=∠BAF=45°,∠AED=∠BFA结合AD=AB即可得到△ADE≌△BAF;
(2)延长AE交BF于点M,由△ABE≌△BCF,可得∠BAE=∠CBF,结合∠CBF+∠ABF=90°可得∠BAE+∠ABM=90°,从而可得∠AMB=90°,由此即可得到AE⊥BF.
试题解析:
(1)由题意可得:
图中以点E或F为顶点的全等三角形有:△ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;
(2)延长AE交BF于点M,
∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴∠AMB=90°,
∴AE⊥BF.



科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
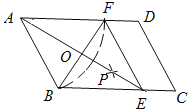
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
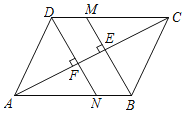
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y= ![]() x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= ![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有
①∠A+∠B=90°
②AB2=AC2+BC2
③ ![]()
④CD2=ADBD.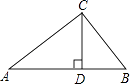
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 ![]() 的概率是 .
的概率是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进![]() ,
,![]() 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现,![]() 型号机器人的单价比
型号机器人的单价比![]() 型号机器人贵600元,3台
型号机器人贵600元,3台![]() 型号机器人比2台
型号机器人比2台![]() 型号机器人贵1200元.
型号机器人贵1200元.
(1)求![]() ,
,![]() 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?
(2)若该快递公司准备用不超过132000元购进![]() ,
,![]() 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进![]() 型号机器人多少台?
型号机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
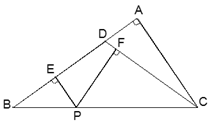
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com